Factoring Trinomials
After studying this lesson, you will be able to:
Steps of Factoring:
1. Factor out the GCF
2. Look at the number of terms:
- 2 Terms: Look for the Difference of 2 Squares
- 3 Terms: Factor the Trinomial
- 4 Terms: Factor by Grouping
3. Factor Completely
4. Check by Multiplying
This lesson will concentrate on the second step of factoring:
Factoring Trinomials.
**When there are 3 terms, we are factoring trinomials. Don't
forget to look for a GCF first.**
Factoring trinomials often requires some trial and error.
Don't get frustrated. Try all possible combinations.
Rules for determining the signs in each factor:
If the Constant Term is Positive, both signs will be
the same (this means that either both will be positive
or both will be negative)
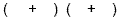 OR OR 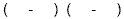
If the Constant Term is Negative, the signs will be
different (this means that one will be positive and one
will be negative)
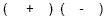 OR OR 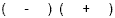
Example 1
Factor x 2 + 7xy + 10y 2
This is a trinomial (has 3 terms). There is no GCF other than
one. So, we start with 2 parentheses:
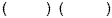
Using our signs rules, we can determine the signs for the
factors. Since the constant term is positive we know the signs
will be the same. Since we want the factors to add up to +7xy the
signs will both have to be positive. Keep this in mind.
1 st : Find the factors of the first term. The factors of x
2 are x and x. These go in the first positions. We can also
go ahead and put in the signs (both positive)
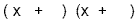
2 nd : Find the factors of the constant term. The factors of
10y 2 are 1y, 10y and 2y, 5y . Remember, we need the
inside/outside combination to add up to the middle term which is
+7xy. Since 2xy and 5xy add up to 7xy, we choose those factors:
(x + 2y ) ( x + 5y)
Check by using FOIL (x + 2y) (x + 5y)  x 2 + 5xy + 2xy + 10y 2
which is x 2 + 7xy + 10y 2 x 2 + 5xy + 2xy + 10y 2
which is x 2 + 7xy + 10y 2
Example 2
Factor x 2 - 8x - 20
This is a trinomial (has 3 terms). There is no GCF other than
one. So, we start with 2 parentheses:
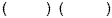
Using our signs rules, we can determine the signs for the
factors. Since the constant term is negative we know the signs
will be different. We want the factors to add up to -8x. Let's
remember that the signs are different. We aren't sure just yet
which sign will be positive and which will be negative.
1 st : Find the factors of the first term. The factors of x 2
are x and x. These go in the first positions. We don't yet put in
the signs because we aren't sure where they go.
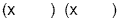
2 nd : Find the factors of the constant term. The factors of
20 are 1, 20 and 2, 10 and 4, 5. Remember, we need the
inside/outside combination to add up to the middle term which is
-8x. We have to remember that we are working with different
signs. Therefore, we're really looking for a pair of factors that
have a difference of 8. Since 2 and 10 have a difference of 8, we
choose those factors. Now we have to decide where to put the
positive and where to put the negative. The 2 and the 10 have to
add up to -8 so we make the 10 negative and the 2 positive.
(x + 2 ) ( x - 10 )
Check by using FOIL (x + 2) ( x - 10 )  x 2 - 10x + 2x - 20 which is x
2 - 8x - 20 x 2 - 10x + 2x - 20 which is x
2 - 8x - 20
Example 5
Factor x 2 + 4x - 12
This is a trinomial (has 3 terms). There is no GCF other than
one. So, we start with 2 parentheses:
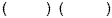
Using our signs rules, we can determine the signs for the
factors. Since the constant term is negative we know the signs
will be different. We want the factors to add up to +4x. Let's
remember that the signs are different. We aren't sure just yet
which sign will be positive and which will be negative.
1st : Find the factors of the first term. The factors of x 2
are x and x. These go in the first positions. We don't yet put in
the signs because we aren't sure where they go.
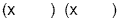
2 nd : Find the factors of the constant term. The factors of
12 are 1, 12 and 2, 6 and 3, 4. Remember, we need the
inside/outside combination to add up to the middle term which is
-+4x. We have to remember that we are working with different
signs. Therefore, we're really looking for a pair of factors that
have a difference of 4. Since 2 and 6 have a difference of 4, we
choose those factors. Now we have to decide where to put the
positive and where to put the negative. The 2 and the 6 have to
add up to +4 so we make the 2 negative and the 6 positive.
(x - 2 ) ( x + 6 ) note : it would be the same thing to write
the factors in this order: (x - 6) (x - 2 )
Check by using FOIL (x - 2) ( x + 6 )  x 2 +6x - 2x - 12 which is x
2 + 4x - 12 x 2 +6x - 2x - 12 which is x
2 + 4x - 12
|