Integers and Substitutions
Commutative properties  a + b = b+ a
· Addition and Subtraction
o If the largest number
o Use your math number sense in order to deal with questions
with only 2 terms Look at the terms and find the largest
value. Whatever sign is of that term will be the value of the
answer(ie positive or negative )
o For questions with multiple terms move one term at a time or a more risky
way is to group terms…problems with this is of replacing the
signs properly
· When terms have multiply Signs
o There is a difference of a subtraction sign and a negation
sign.
o An equation cannot have two signs ( + , - ) side-by-side. We
must change the signs so that there is only one sign between
them. There are some simple rules that we must follow
o Two minus’s become a plus
o Two plus’s become a plus
o One minus and one plus becomes a minus
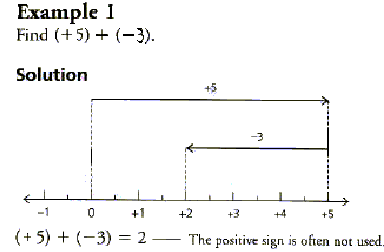
- Ex - 20 - (-5) = -20 + 5 = -15
- Ex 7 + (+11) = 18
- Ex -4 - (-7) = -4 + 7 = 3
o This can also be done while using a number line
· Multiplying and Dividing
o A negative times a negative gives a positive, a positive
times a positive gives a positive, while a negative times a
positive gives a negative. If they are both the same then
positive, but if they are different then negative. If they are an
even number of negatives then it will be positive, but if there
are an odd number of negatives, then it will be negative.
o After the operation(s) if there is an even number of
negative signs the answer is positive (or if all positive no
worries)
o if there is an odd number of negative signs then the answer
is negative
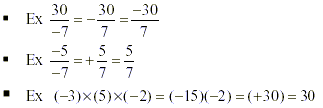
Substitution
· The act of replacing an unknown with a known value.
o 5x 2 - 7y when x is 2 and y is 7
o when we replace an unknown with a value we put the new
quantity in with brackets. This way we can show others what
values we have replaced.
o Once all unknowns are replaced with given information we
follow normal BEDMAS rules.
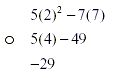
· Sometimes only some of the variables are accounted for. So
we only replace those that we know. We cannot replace or get rid
of variables.
|
