Intersections of Lines and Conics
Some times it is important to find out how a conic can intersect with a line. There are 3
possible sets of solutions (remember a set of solutions are the points that satisfy the given
equation). The 3 cases are
• No solution. This means that the line does not intersect the conic. There will
no real points.
• 1 solution. The line only crosses the conic at a single point. There will be
only one unique set of points found that satisfy the equations
• 2 solutions. The line crosses the conic in two places. There will be 2 sets of
unique points that satisfy the equation.
The best way to solve the sets in these cases is by substitution, since it is easy to
manipulate the equation of a line.
Example 1
Find the point of intersection between the line y = x - 1 and x2 +
y2 = 25.
Solution
| y |
= x - 1 |
| x2 + y2 |
= 25 |
| x2 + (x - 1)2
|
= 25 |
| x2 + x2 -
2x + 1 |
= 25 |
| 2x2 - 2x - 24 |
= 0 |
| x2 - x - 12 |
= 0 |
| (x - 4)(x + 3) |
= 0 |
| |
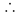x = 4; x = -3 |
Using the two values of x, substitute into one of the equations above to find the
corresponding y values.
Therefore the two solutions are (4,3) and (-3, -4)
Example 2
Find the point(s) of intersection of the parabola y - 4 = -(x + 1)2 and the line
y = -4x + 4.
Solution:
| y - 4 |
= -(x + 1)2 |
| -4x + 4 - 4 |
= -(x2 + 2x + 1) |
| -4x |
= -x2 - 2x - 1 |
| x2 - 2x + 1 |
= 0 |
| (x - 1)2 |
= 0 |
| x2 - x - 12 |
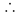x = 1 |
Sub the value of x into the equation for the y value. it is 0. The point of intersection is
(1, 0).
When you get to the point when you have to factor, do not hesitate to use the quadratic
equation to solve more complex equations.
|
