Solving Equations with Log Terms on Each Side
When solving equations with two or more logs it is often necessary to use
the properties of logarithms.
| Log of a Product Property:
Log of a Quotient Property:
Log of a Power Property: |
logb u · v
= logb u + logb v
logb
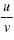= logb u - logb v
logb un = n · logbu |
Here is another useful property. It says that if the logs of two quantities are
equal, then the quantities are equal.
Property —
Logarithmic Equality
If logb x = logb y, then x = y.
Here, x > 0, y > 0, b > 0 and b ≠ 1.
In the following examples, we will first use the properties of logarithms to
rewrite each equation so there is one log on each side. Then, we will use
the Principal of Logarithmic Equality.
Example 1
Solve: log 4 + log x = log 14
| Solution
Use the Log of a Product Property.
Use the Principal of Logarithmic Equality.
Divide both sides by 4. |
log 4 + log x log 4x
4x
x |
= log 14 = log 14
= 14
= 3.5 |
So, the solution is x = 3.5.
Note:
To check the solution of
log 4 + log x = log 14, substitute
3.5 for x and simplify.
| Is
Is
Is |
log 4 + log x
log 4 + log 3.5
0.602 + 0.544
1.146 |
= log 14 = log 14
?
= 1.146 ?
= 1.146 = Yes |
Because we must round the values of the
logs, in some cases the two sides of the
equation will not simplify to exactly the
same result. However, the results should
be very close.
Example 2
Solve: log (x + 4) - log 6 = log (x - 11).
| Solution |
log (x + 4) - log 6 |
= log (x - 11) |
| Use the Log of a Quotient Property. |
 |
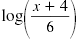= log (x - 11) |
| Use the Principal of Logarithmic Equality.
|
 |
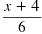= x - 11 |
| Multiply both sides by 6.
Subtract x from both sides.
Add 66 to both sides.
Divide both sides by 5. |
x + 4
4
70
14 |
= 6x - 66
= 5x - 66
= 5x
= x |
So, the solution is x = 14. We leave the check to you.
|
