The parabola
While we have studied the parabola earlier, we have not looked
at it as a set of points lying in a plane. Using the two stacked
cones, the parabola is another conic section, involving one of
the cones.
The parabola is the set of points that from a point P to a
fixed point F, equals the distance from P to a fixed line l.
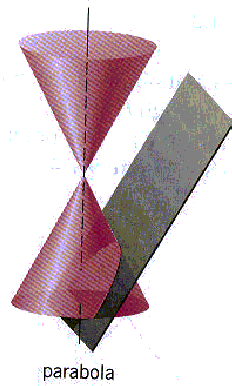
One other condition is also true, and that is PD = PF
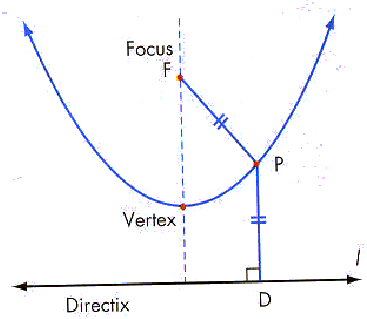
· The point F is the focus, and the line l is a fixed line
called the directrix.
· The vertex of the parabola lays ½ between the directrix
and the focus.
o The directrix
· The parabola will never cross the directrix, and hence
always opens away from this line
Example 1
A parabola has a focus at F(0,3) and a directrix Y = -3. Find
the equation of the parabola.
Solution:
The middle from the focus and the directrix is at the origin.
We know that any point on the parabola will be of the form P( x,
y ). Any point on the directrix will be of the form D( x, 3).
Since we know PD = PF, we can use this information to create the
equation.

In general, if the focus is F(0, p) and the directrix is y = -p
then the equation of the parabola is 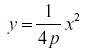
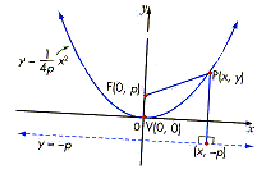
| The standard form of the
equation of a parabola with vertex V(h, k) and a
horizontal directrix is 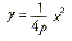
The vertex is V(0, 0).
If p > 0, the parabola opens up.
If p < 0, the parabola opens down.
The focus is F(0, p).
The equation of the directrix is y = - p.
The equation of the axis of symmetry is the y-axis.
|
The standard form of the
equation of a parabola with vertex V(h, k) and a vertical
directrix is 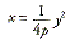
The vertex is V(0, 0).
If p > 0, the parabola opens right.
If p > 0, the parabola opens left.
The focus is F(p, 0).
The equation of the directrix is x = - p.
The equation of the axis of symmetry is the x-axis.
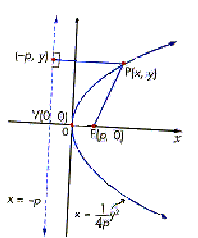
|
For parabolas in non-standard position:
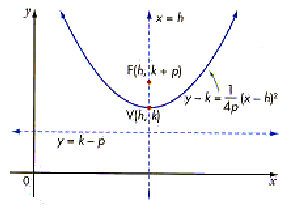
| The standard form of the
equation of a parabola with vertex V(h, k) and a
horizontal directrix is 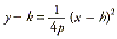
The vertex is V(h, k).
If p > 0, the parabola opens up.
If p < 0, the parabola opens down.
The focus is F(h, k + p).
The equation of the directrix is y = k - p.
The equation of the axis of symmetry is x = h.
|
The standard form of the
equation of a parabola with vertex V(h, k) and a vertical
directrix is 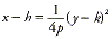
The vertex is V(h, k).
If p > 0, the parabola opens right.
If p > 0, the parabola opens left.
The focus is F(h + p, k).
The equation of the directrix is x = h - p.
The equation of the axis of symmetry is y = k.
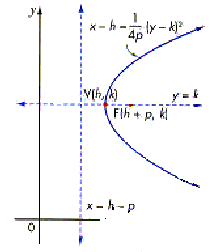
|
|