Using the Quadratic Formula
The quadratic formula can be used to solve any quadratic equation.
Equation 1
Two rational solutions
Solve x2 + 2x - 15 = 0 using the quadratic formula.
Solution
To use the formula, we first identify the values of a, b, and c:
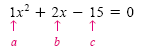
The coefficient of x2 is 1, so a = 1. The coefficient of 2x is 2, so b
= 2. The constant
term is -15, so c = -15. Substitute these values into the quadratic formula:
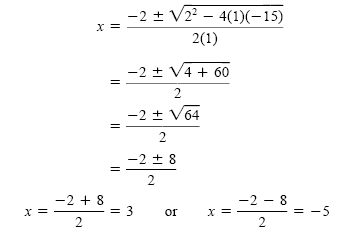
Check 3 and -5 in the original equation. The solution set is {-5, 3}.
Caution
To identify a, b, and c for the quadratic formula, the equation
must be in the standard form ax2 + bx + c = 0. If it is not in that form, then you
must first rewrite the equation.
Example 2
One rational solution
Solve 4x2 = 12x - 9 by using the quadratic formula.
Solution
Rewrite the equation in the form ax2 + bx + c = 0 before identifying a, b, and c:
4x2 - 12x + 9 = 0
In this form we get a = 4, b = -12, and c = 9.
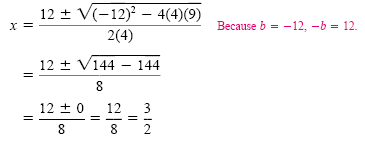
Check
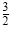in the original equation. The solution set is
 .
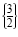Because the solutions to the equations in Examples 1 and 2 were rational numbers,
these equations could have been solved by factoring. In the next example the
solutions are irrational.
Example 3
Two irrational solutions
Solve 2x2 + 6x + 3 = 0.
Solution
Let a = 2, b = 6, and c = 3 in the quadratic formula:
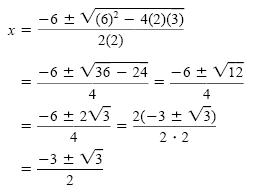
Check these values in the original equation. The solution set is
 .
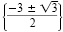Example 4
Two imaginary solutions, no real solutions
Find the complex solutions to x2 + x + 5 = 0.
Solution
Let a = 1, b = 1, and c = 5 in the quadratic formula:
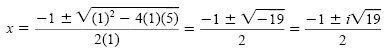
Check these values in the original equation. The solution set is
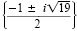 . There
are no real solutions to the equation.
Number of Solutions to a Quadratic Equation
The quadratic equations in Examples 1 and 3 had two real solutions each. In each of
those examples the value of b2 - 4ac was positive. In Example 2 the quadratic
equation had only one solution because the value of b2 - 4ac was zero. In Example
4 the quadratic equation had no real solutions because b2 - 4ac was negative.
Because b2 - 4ac determines the kind and number of solutions to a quadratic
equation, it is called the discriminant.
Number of Solutions to a Quadratic Equation
The quadratic equation ax2 + bx + c = 0 with a
≠ 0 has
two real solutions if b2 - 4ac >
0,
one real solution if b2 - 4ac = 0, and
no real solutions (two imaginary solutions) if b2 - 4ac < 0.
Example 5
Using the discriminant
Use the discriminant to determine the number of real solutions to each quadratic
equation.
a) x2 - 3x - 5 = 0
b) x2 = 3x - 9
c) 4x2 - 12x + 9 = 0
Solution
a) For x2 - 3x - 5 = 0, use a = 1, b = -3, and c = -5 in b2
- 4ac:
b2 - 4ac = (-3)2 - 4(1)(-5) = 9 + 20 = 29
Because the discriminant is positive, there are two real solutions to this quadratic
equation.
b) For x2 - 3x + 9 = 0, use a = 1, b = -3, and c = 9 in b2
- 4ac:
b2 - 4ac = (-3)2 - 4(1)(9) = 9 - 36 = -27
Because the discriminant is negative, the equation has no real solutions. It has
two imaginary solutions.
c) For 4x2 - 12x + 9 = 0, use a = 4, b = -12, and c = 9 in b2
- 4ac:
b2 - 4ac = (-12)2 - 4(4)(9) = 144 - 144 = 0
Because the discriminant is zero, there is only one real solution to this quadratic
equation.
|
