Multiplying And Dividing Fractions
Fractions are used when we don't have a whole number of something. When you combine fractions together, you often need to multiply and divide
fractions.
Multiplication
To multiply fractions, convert all mixed numbers to improper fractions, and write them
on a common bar.
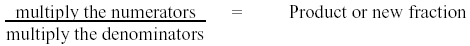
Example:
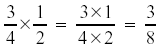
To reduce your labor, cancel factors that appear in both numerator and denominator. That
is, if the same number appears in both the top and bottom then you can cross out the pair.
This keeps the numbers smaller and makes them easier to use.
Example:
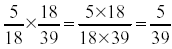
Identity Element of Multiplication
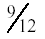 and and
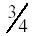 are equivalent fractions. are equivalent fractions.
To understand this, we need to consider the identity element of multiplication:
Whenever the same non-zero number appears in both the numerator and denominator,
the fraction is equal to 1.
Thus,
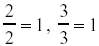 , and even , and even
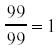 . .
The number 1 is the identity element of multiplication. That means
whenever we multiply a number by 1, we get the same number.
Think: What is the identity element of division?
To prove that
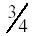 and and
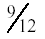 are equivalent fractions, we will show how are equivalent fractions, we will show how
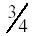 has been
multiplied by 1 to get the new fraction: has been
multiplied by 1 to get the new fraction:
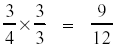
The identity element can be written in many forms. Note that anything (except zero)
divided by itself is 1, so any of these forms could be used for the identity element of
multiplication:
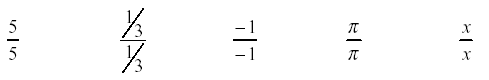
Choose the form of the identity element that simplifies your calculations.
One is the identity element for multiplication of numbers, since a ×1
= 1 × a = a for all
values of a.
|