Writing Fractions as Decimals
Objective Learn how to write fractions as
decimals, using long division.
This lesson is an excellent application of long division and
division of decimals. It is important to be able to write
fractions as decimals. It is more difficult to compare and
perform addition and subtraction on fractions than on decimals.
Fractions Represent Division
Remember that fractions really represent the division of one
integer by another integer. For example, 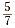 represents the division
of 5 by 7. represents the division
of 5 by 7.
Writing Decimals as Fractions
The division represented by a fraction can be performed to
produce the decimal equivalent of the fraction.
Key Idea
To write a fraction in decimal form, divide the numerator by
the denominator.
Example 1
Write each fraction as a decimal.

Solution
a. First write 3 as 3.0, and then divide by
5.
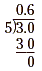
So, 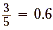 . .
b. Write 1 as 1.0 and then divide by 2.
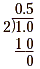
So, 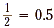 . .
Sometimes it is necessary to add more than one zero at the end
of the decimal created from the numerator. One additional zero is
added and the division continues each time a division step
results in a remainder. This is shown in the following examples.
Example 2
Write each fraction as a decimal.

Solution
a. When we try to write 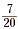 as a decimal, with 7
written as 7.0, we get as a decimal, with 7
written as 7.0, we get
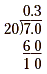
Since the division in this step resulted in a remainder of 10,
we add another zero to the dividend, 7.0, and continue dividing.
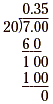
The division has no remainder, so 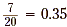 . .
b. Begin by rewriting 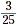 as the division 3.0 ÷
25. as the division 3.0 ÷
25.
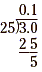
Since there is a remainder, add another zero and continue
dividing.
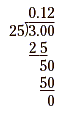
So, 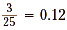 . .
The two previous examples show a pattern in which for
single-digit denominators only one zero is needed for the
division, and for double-digit denominators two zeros are needed.
The following example shows that the pattern was only
coincidental.
Example 3
Write 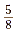 as a decimal. as a decimal.
Solution
Write 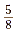 as the division 5.0 ÷
8. as the division 5.0 ÷
8.
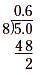
Add another zero to the dividend and continue dividing.
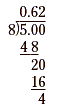
Add another zero and continue dividing.
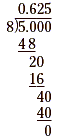
So, 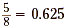 . .
Terminating and Repeating Decimals
Sometimes the division never comes out evenly no matter how
many zeros we add.
Example 4
Write 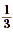 as a decimal. as a decimal.
Solution
Use long division as in Examples 1–3.
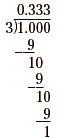
The remainder at each step will always be 1 and the next digit
in the quotient will always be 3. So the quotient is 0.333…
(the dots mean that the pattern continues indefinitely), which
can also be written as 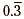 (the bar over the 3
means that the digit repeats). (the bar over the 3
means that the digit repeats).
When the division never comes out evenly, the fraction cannot
be written as a terminating decimal (a decimal
that ends). However, in these situations there is always a
pattern of digits that eventually repeats, and it may involve
more than just a single digit, as in Example 4.
Expressions such as 0.33333… and 0.090909… are
called repeating (or nonterminating ) decimals
because one or more digits repeat.
|