Free Algebra
Tutorials!


	Home
	Miscellaneous Equations
	Operations with Fractions
	Undefined Rational Expressions
	Inequalities
	Writing Equations for Lines Using Sequences
	Intersections of Lines and Conics
	Graphing Linear Equations
	Solving Equations with Log Terms and Other Terms
	Quadratic Expresions - Complete Squares
	Adding and Subtracting Fractions with Like Denominators
	Multiplying a Fraction by a Whole Number
	Solving Equations with Log Terms and Other Terms
	Solving Quadratic Equations by Factoring
	Locating the Solutions of the Quadratic Equation
	Properties of Exponents
	Solving Equations with Log Terms on Each Side
	http:
	Graphs of Trigonometric Functions
	Estimating Products and Quotients of Mixed Numbers
	Inequalities
	The circle
	Adding Polynomials
	Adding Fractions with Unlike Denominators
	Factoring Polynomials
	Linear Equations
	Powers of Ten
	Straight Lines
	Dividing With Fractions
	Multiplication Property of Equality
	Rationalizing Denominators
	Multiplying And Dividing Fractions
	Distance Between Points on a Number Line
	Solving Proportions Using Cross Multiplication
	Using the Quadratic Formula
	Scientific Notation
	Imaginary Numbers
	Values of Symbols for Which Fractions are Undefined
	Graphing Equations in Three Variables
	Writing Fractions as Decimals
	Solving an Equation with Two Radical Terms
	Solving Linear Systems of Equations by Elimination
	Factoring Trinomials
	Positive Rational Exponents
	Adding and Subtracting Fractions
	Negative Integer Exponents
	Rise and Run
	Brackets
	Multiplying Square Roots
	Multiplying Polynomials
	Solving Systems of Linear Inequalities
	Multiplication Property of Radicals
	A Quadratic within a Quadratic
	Graphing a Linear Equation
	Calculations with Hundreds and Thousands
	Multiplication Property of Square and Cube Roots
	Solving Equations with One Log Term
	The Cartesian Coordinate Plane
	Equivalent Fractions
	Adding and Subtracting Square Roots
	Solving Systems of Equations
	Exponent Laws
	Solving Quadratic Equations
	Factoring Trinomials
	Solving a System of Three Linear Equations by Elimination
	Factoring Expressions
	Adding and Subtracting Fractions
	The parabola
	Computations with Scientific Notation
	Quadratic Equations
	Finding the Greatest Common Factor
	Introduction to Fractions
	Simplifying Radical Expressions Containing One Term
	Polynomial Equations
	Graphing and Intercepts
	The Number Line
	Adding and Subtracting Rational Expressions with Different Denominators
	Scientific Notation vs Standard Notation
	Powers
	Factoring by Grouping
	Extraneous Roots
	Variables and Expressions
	Linera Equations
	Integers and Substitutions
	Squares and Square Roots
	Adding and Subtracting Rational Expressions with Different Denominators
	Solving Linear Inequalities
	Expansion of a Product of Binomials
	Powers and Exponents
	Finding The Greatest Common Factor
	Quadratic Functions
	The Intercepts of a Parabola
	Solving Equations Containing Rational Expressions
	http:
	Subtracting Polynomials
	Solving Equations
	Adding Fractions with Unlike Denominators
	Solving Systems of Equations by Substitution
	Solving Equations
	Product and Quotient of Functions

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Quadratic Equations by Factoring

Quadratic Equation

If a, b, and c are real numbers, with a ≠ 0, then the equation ax² + bx + c = 0 is called a quadratic equation.

Keep the following strategy in mind when solving equations by factoring.

Strategy for Solving Equations by Factoring

1. Write the equation with 0 on the right-hand side.

2. Factor the left-hand side.

3. Use the zero factor property to get simpler equations. (Set each factor equal to 0.)

4. Solve the simpler equations.

5. Check the answers in the original equation.

Example

Solving a quadratic equation by factoring

Solve each equation.

a) 10x² = 5x

b) 3x - 6x² = -9

Solution

a) Use the steps in the strategy for solving equations by factoring:

10x² = 5x			Original equation
10x² - 5x = 0			Rewrite with zero on the right-hand side.
5x(2x - 1) = 0			Factor the left-hand side.
5x = 0	or	2x - 1 = 0	Zero factor property
x = 0	or		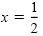Solve for x.

The solution set is 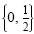. Check each solution in the original equation.

b) First rewrite the equation with 0 on the right-hand side and the left-hand side in order of descending exponents:

3x - 6x² = -9			Original equation
-6x² + 3x + 9 = 0			Add 9 to each side.
2x² - x - 3 = 0			Divide each side by -3.
(2x - 3)(x + 1)			Factor.
2x - 3 = 0	or	x + 1 = 0	Zero factor property
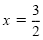	or	x = -1	Solve for x.

The solution set is 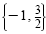. Check each solution in the original equation.

Caution

If we divide each side of 10x² = 5x by 5x, we get 2x = 1, or 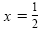. We do not get x = 0. By dividing by 5x we have lost one of the factors and one of the solutions.