Straight Lines
Straight Line Graphs
A general linear function has the form y = mx + c , where m, c
are constants.
Example 1
A straight line passes through the two points P ( x, y ) and Q
( x, y ) with coordinates P (0 , 2) and Q (1 , 5) . Find the
equation of this straight line.
Solution
The general equation of a straight line is y = mx + c. Since
the line passes through the points P , with coordinates x = 0 , y
= 2, and Q , with coordinates x = 1, y = 5, these coordinates
must satisfy this equation, i.e.
2 = m × 0 + c
1 = m × 5 + c
Solving these equations gives c = 2 and m = 3 , i.e. the line
is y = 3 x + 2 .
Exercise 1
In each of the following find the equation of the straight
line through the given pairs of points.
(a) The points P (0 , - 3) and Q (2 , 1) .
(b) The points P (0 , 4) and Q (1 , 3) .
Solution
(a) The general equation of a straight line
is y = mx + c . Since the line passes through the points P and Q
, the coordinates of both points must satisfy this equation. The
point P has coordinates x = 0 , y = - 3 and the point Q has
coordinates x = 2 , y = 1 . These satisfy the pair of
simultaneous equations
- 3 = m × 0 + c
1 = m × 2 + c
Solving these equations gives c = - 3 and m = 2 , i.e. the
line is y = 2 x - 3 .
(b) The general equation of a straight line
is y = mx + c . Since the line passes through the points P and Q
, the coordinates of both points must satisfy this equation. The
point P has coordinates x = 0 , y = 4 and the point Q has
coordinates x = 1 , y = 3. These satisfy the pair of simultaneous
equations
4 = m × 0 + c
3 = m × 1 + c
Solving these equations gives c = 4 and m = - 3 , i.e. the
line is y = - 3 x + 4 .
Gradient of a Straight Line
The gradient of a straight line is defined as follows. Suppose
that two points P, Q, on the line have coordinates P( x1
, y1 ) and Q( x2 , y2 ) .
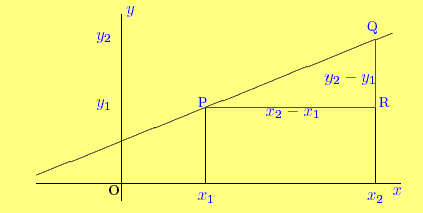
The gradient of the line is (see diagram above)
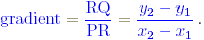
Exercise 2
Find the gradient of the line through the points P(3, 9) and
Q(2, 3).
Solution
For P(3 , 9) , Q(2 , 3) , the gradient is given by
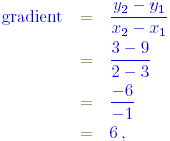
so that m = 6 in this case.
Intercepts of a Straight Line
By putting x = 0 into the equation y = mx + c , the point
where the straight line crosses the y axis is found to be y = c .
This is known as the intercept on the y axis . The intercept on
the x axis, i.e. when y = 0, is at
0 = mx + c
- c = mx
- c/m = x .
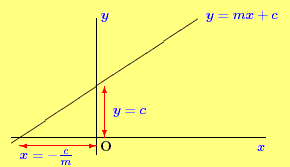
The x and y intercepts.
Example 2
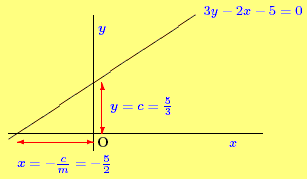
By rearranging the equation 2 y - 3 x - 5 = 0 , show that it
is a straight line and find its gradient and intercept. Sketch
the line.
Solution
Rearranging the equation,
3 y - 2 x - 5 = 0
3 y = 2 x + 5
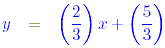
(Equation of a straight line with m = 2 / 3 and c = 5 / 3.)
Exercise 3
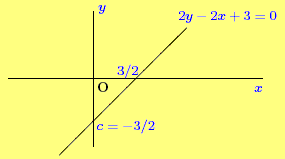
The equation 2 y - 2 x + 3 = 0 represents a straight line. By
rearranging it, find its gradient and the intercepts on the y and
x axis. Sketch the straight line it represents.
Solution
For the equation 2 y - 2 x + 3 = 0,
2 y - 2 x + 3 = 0
2 y = 2 x - 3
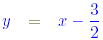
so that m = 1 and c = - 3 / 2. The intercept on the x axis is
- c/m = - ( - 3 / 2) / 1 = 3 / 2.
Quiz
A straight line has the equation 3 x + y +3 = 0. If P is the
point where the line crosses the x-axis and Q is the point where
it crosses the y-axis, which of the following pair is P,Q?

Solution
The line crosses the x axis when y = 0 . Putting this into the
equation of the line, 3 x + y + 3 = 0 , gives
3 x + 0 + 3 = 0
3 x = - 3 x = - 1.
Thus P ( - 1 , 0) is the first point.
The line crosses the y axis when x = 0. Putting this into the
equation of the line,
3 × (0) + y + 3 = 0
y + 3 = 0 y = - 3.
Thus Q (0 , - 3) is the second point.
|