Solving an Equation with Two Radical Terms
Example
Solve for x:
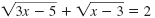
| Solution Step 1 Isolate a radical term.
Subtract
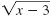 from both sides. from both sides.
Step 2 Apply the Principle of Powers.
|
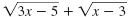
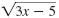 |
= 2
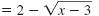 |
| Square both sides. |
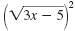 |
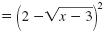 |
| Step 3 Solve the resulting equation.
Write the right side as a product. |
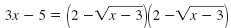 |
| FOIL the right side.
|
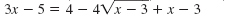 |
| Isolate the remaining radical term.
|
2x - 6 |
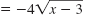 |
| Divide both sides by 2.
|
x - 3 |
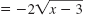 |
| Square both sides.
|
(x - 3)2 |
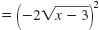 |
| Write the left side as a product.
Simplify.
Write in standard form.
Factor.
Use the Zero Product Property.
Solve for x. Step 4 Check the solution. |
(x - 3)(x - 3)
x2 - 6x + 9
x2 - 10x - 21
(x - 3)(x - 7)
x - 3 = 0 or x - 7
x = 3 or x |
= 4(x - 3)
= 4x - 12
= 0
= 0
= 0
= 7 |
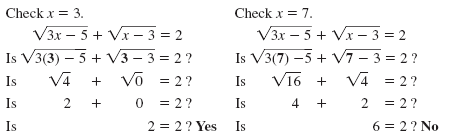
Since x = 7 does not check, the only solution is x
= 3.
Note:
We divide both sides by 2 rather than 4 in
order to avoid introducing fractions into
the equation.
One way to simplify
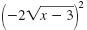 is: is:
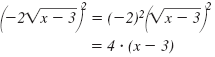
|