Solving Equations
When fractions occur we can sometimes transform the equation
to one that does not involve fractions.
Example
Find the solution to the equation
(4 x/ 5) - (7 / 4) = ( x/ 5) + ( x/ 4) .
Solution
The least common multiple of the denominators in the equation
is 4 × 5 = 20 and we proceed as follows:
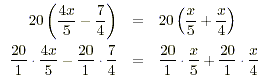
16 x - 35 = 4 x + 5 x
16 x - 35 = 9 x
adding 35 to both sides and subtracting 9 x from both sides
leads to
7 x = 35 so x = 5 is the solution to the equation .
Exercise
Find the solution to each of the following equations.
(a) 5 x - 6( x - 5) = 2( x + 5) + 5( x - 4)
(b) ( x + 15)( x - 3) - ( x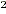 - 6
x + 9) = 30 - 15( x - 1) - 6
x + 9) = 30 - 15( x - 1)
(c) ( x - 2) / 2 + ( x + 10) / 9 = 5
Solution
(a)
5 x - 6( x - 5) = 2( x + 5) + 5( x - 4)
5 x - 6 x + 30 = 2 x + 10 + 5 x - 20
- x + 30 = 7 x - 10
30 = x + 7 x - 10
30 = 8 x - 10
30 + 10 = 8 x
8 x = 40
x = 5
(b) First, using FOIL , we expand
( x + 15)( x - 3) = x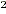 - 3
x + 15 x - 45 = x - 3
x + 15 x - 45 = x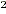 + 12 x - 45 + 12 x - 45
Now we have
( x + 15)( x - 3) - ( x14 2 - 6 x + 9) = 30 - 15( x - 1)
x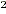 + 12 x - 45 - x + 12 x - 45 - x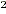 + 6
x - 9 = 30 - 15 x + 15 + 6
x - 9 = 30 - 15 x + 15
18 x - 54 = 45 - 15 x
18 x + 15 x - 54 = 45
33 x - 54 = 45
33 x = 45 + 54
33 x = 99
x = 3
(c) This time we multiply both sides by 2 ×
9 .
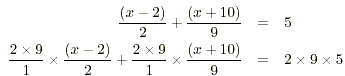
9( x - 2) + 2( x + 10) = 90
9 x - 18 + 2 x + 20 = 90
11 x + 2 = 90
11 x = 88
x = 8
Quiz
Which of the following is the solution to the equation (x -
4)/7 = (x - 10)/5 ?
(a) 11 (b) - 10 (c) 19 (d) 25
Solution:
The highest common factor of the denominators is 5 × 7 = 35 .
Multiplying both sides of the equation by this
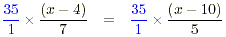
5( x - 4) = 7( x - 10)
5 x - 20 = 7 x - 70
5 x - 20 + 70 = 7 x - 70 + 70
5 x + 50 = 7 x
50 = 7 x - 5 x = 2 x
x = 25
so that x = 25 is the solution. This can be checked by putting
this value into the original equation and showing that each side
will have the value 3 .
|