Powers
Introduction
A power, or an exponent, is used to write a product of numbers
very compactly. In this leaflet we remind you of how this is
done, and state a number of rules, or laws, which can be used to
simplify expressions involving indices.
1. Powers, or exponents
We write the expression 3×3×3×3 as 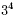
We read this as "three to the power four". Similarly
z × z × z = 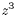
We read this as " z to the power three" or " z
cube".
In the expression 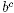 the exponent is c and the number b is called the
base. Your calculator will probably have a button to evaluate
powers of numbers. It may be marked the exponent is c and the number b is called the
base. Your calculator will probably have a button to evaluate
powers of numbers. It may be marked 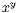 . Check this,
and then use your calculator to verify that . Check this,
and then use your calculator to verify that
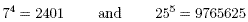
Exercises
1. Without using a calculator work out the value of
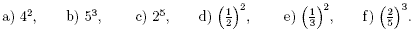
2. Write the following expressions more concisely by using
powers.
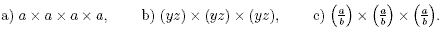
Answers
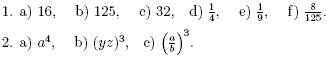
2. The laws of exponents
To manipulate expressions involving exponents we use rules
known as the laws of exponents. The laws should be used precisely
as they are stated - do not be tempted to make up variations of
your own! The three most important laws are given here:
First law 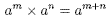
When expressions with the same base are multiplied, the
exponents are added.
Example
We can write 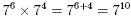
You could verify this by evaluating both sides separately.
Example
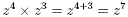
Second Law 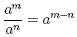
When expressions with the same base are divided, the exponents
are subtracted.
Example
We can write
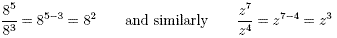
Third law 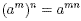
Note that m and n have been multiplied to yield the new
exponent mn.
Example
It will also be useful to note the following important
results:

Exercises
1. In each case choose an appropriate law to simplify the
expression:
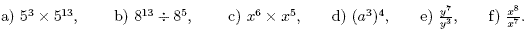
2. Use one of the laws to simplify, if possible, 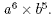
Answers
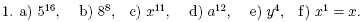
2. This cannot be simplified because the bases are not the
same.
|