Adding and Subtracting Fractions

FRACTION: If a and b are real numbers then the expression

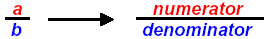
is called a fraction. The top number a is called the numerator and the bottom number b is called the denominator. Division by zero is not allowed, so b ≠ 0 or the result is undefined.

Adding fractions

Remember that for addition all fractions must have common denominators. [The result must be checked to see if it will reduce to simpler form.]

I. Adding fractions with common denominators:

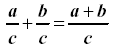Keep the common denominator then add the numerators. Follow all of the properties for “signed numbers”.

Example:

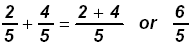
II. Adding fractions that do not have common denominators:

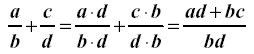
Example:

Factor the denominators and find the least common denominator (LCD). Raise both (or all) fractions to have the LCD, then add the new numerators.

Example:

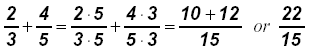
Equivalent Fractions: If the numerator and denominator are multiplied by a common factor the resulting expression is an equivalent fraction that has the same numerical value.

Multiply fractions: Multiply numerators times numerators and denominators times denominators.

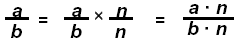
Add Fractions with Different Denominators: If the fractions do not have common denominators [Factor the denominators and find the LCD. ] RAIISE all fractions to have common denominators,

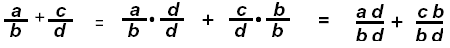
then add the resulting numerators.

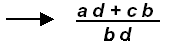
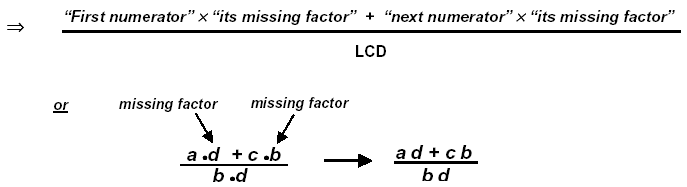
→ Another approach to this is to write the LCD in the denominator with a long “overbar” -- write the “first numerator” then compare its denominator with the LCD (the other factors will be the “missing factor”) which will be multiplied times the numerator.

→ Next, remember that the “sign goes with the number that follows it” and write the “next signed numerator” – compare its denominator with the LCD for the “missing factor” to multiply times that numerator. Repeat for all fractions in the sum.

Learn this well. These steps will also work with algebraic fractions that contain variables so you will probably want to “bookmark” these pages.

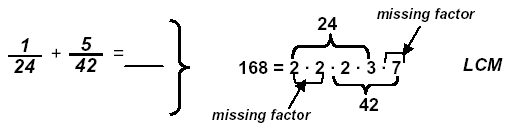
Example:

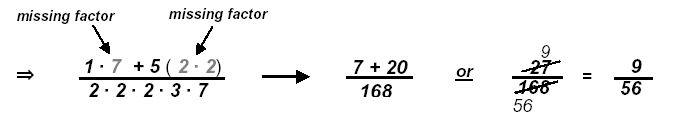
Adding mixed numbers – integers and fractions

One of the problems that students have difficulty with occurs when one of the “addends” is an integer. They forget that all integers have a denominator of 1.

Example 2:

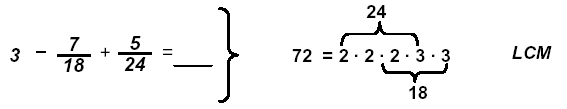
III. In algebra some of the factors may be letters, or variables, which must be treated as “prime factors”. They will be left in the result as “literal sums”.
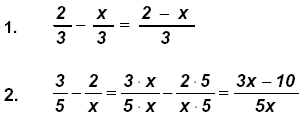