Simplifying Radical Expressions Containing One
Term
Example
Simplify:
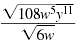
Solution
This radical expression is not in simplified form because it has a radical in
its denominator.
To begin, we will write the expression as a quotient under a single radical
symbol.
Then we will try to simplify that quotient so that it can be written without
a denominator.
| |
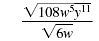 |
| Use the Division Property of
Radicals to write the quotient
under one radical symbol. |
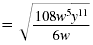 |
| Simplify the radicand. |
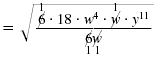 |
| We have rewritten the radicand
without a denominator. However,
the radicand has some factors that
are perfect squares. |
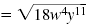 |
| Factor the radicand. Use perfect
square factors when possible.
|
 |
| Write as a product of radicals.
Place each perfect square under
its own radical symbol. |
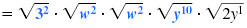 |
| Simplify the square root of each
perfect square. |
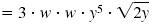 |
| Multiply the factors outside the
radical symbol. |
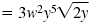 |
| So, |
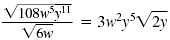 |
|