Solving Systems of Equations by Substitution
Solving a system by graphing is certainly limited by the accuracy of the graph. If the
lines intersect at a point whose coordinates are not integers, then it is difficult to
determine those coordinates from the graph. The method of solving a system by
substitution does not depend on a graph and is totally accurate. For substitution we
replace a variable in one equation with an equivalent expression obtained from the
other equation. Our intention in this substitution step is to eliminate a variable and
to give us an equation involving only one variable.
Example 1
An independent system solved by substitution
Solve the system by substitution:
2x + 3y = 8
y + 2x = 6
Solution
We can easily solve y + 2x = 6 for y to get y = -2x + 6. Now replace y in the
first equation by -2x + 6:
| 2x + 3y |
= 8 |
|
| 2x + 3(-2x + 6) |
= 8 |
Substitute -2x + 6 for y. |
| 2x - 6x + 18 |
= 8 |
|
| -4x |
= -10 |
|
| x |
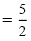 |
|
To find y, we let
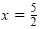 in the equation y = -2x + 6:
in the equation y = -2x + 6:
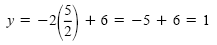
The next step is to check
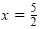 and y
= 1 in each equation. If and y
= 1 in each equation. If
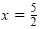 and y
= 1
in 2x + 3y = 8, we get and y
= 1
in 2x + 3y = 8, we get
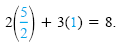
If
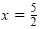 and y
= 1 in y + 2x = 6, we get and y
= 1 in y + 2x = 6, we get
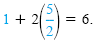
Because both of these equations are true, the solution set to the system is
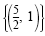 . The equations of this system are independent. . The equations of this system are independent.
Example 2
An inconsistent system solved by substitution
Solve by substitution:
x - 2y = 3
2x - 4y = 7
Solution
Solve the first equation for x to get x - 2y = 3 . Substitute 2y + 3 for x in the
second equation:
| 2x - 4y |
= 7 |
| 2(2y + 3) |
= 7 |
| 4y + 6 - 4y |
= 7 |
| 6 |
= 7 |
Because 6 = 7 is incorrect no matter what values are chosen for x and y, there is no
solution to this system of equations. The equations are inconsistent. To check, we
write each equation in slope-intercept form:
| x - 2y |
= 3 |
2x - 4y |
= 7 |
| -2y |
= -x + 3 |
-4y |
= -2x + 7 |
| y |
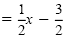 |
y |
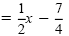 |
The graphs of these equations are parallel lines with different y-intercepts. The
solution set to the system is the empty set, Ø.
|