Finding The Greatest Common Factor (GCF)
In order to find the greatest common factor we use prime
numbers. A prime number is an integer that is greater than one
and has no factors other than itself and one.
Examples: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
. .
I. Factoring A Number Into Primes
1. Check to see if the first prime number, 2, divides evenly
into the given number.
2. If it doesn't divide evenly, try the next prime number, 3.
Continue until you find a prime factor.
3. Rewrite the given number as a product of the prime factor
and the result from division.
4. Repeat steps 1-3 on the number resulting from division.
5. Repeat steps 1-4 until the given number is written as a
product of primes.
Example:
| 1260 |
1260 |
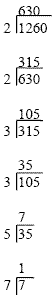 |
2 * 630 |
| 2 * 2 * 315 |
| 2 * 2 * 3 * 105 |
| 2 * 2 * 3 * 3 * 35 |
| 2 * 2 * 3 * 3 * 5 * 7 |
The prime factorization of 1260 is 2 * 2 * 3 * 3 * 5 * 7,
which are the numbers along the left side in the above divisions.
II. Finding The Greatest Common Factor
1. Factor each number completely into primes.
2. Look at the common factors for the two numbers.
3. Multiply the common factors together to get the GCF.
Example:
| 252 |
90 |
| 2 * 126 |
2 * 45 |
| 2 * 2 * 63 |
2 * 3 * 15 |
| 2 * 2 * 3 * 21 |
2 * 3 * 3 * 5 |
| 2 * 2 * 3 * 3 * 7 |
|
| |
|
| 2 * 2 * 3 * 3 * 7 |
2 * 3 * 3 * 5 |
The underlined factors are the ones common to both 252 and 90.
Now multiply the common factors: 2 * 3 * 3 = 18.
The greatest common factor of 252 and 90 is 18.
We can also use this method to find the GCF of two
algebraic expressions.
Example:
| 60x 2 y |
210xy 2 |
| 2 * 30x 2y |
2 * 105xy 2 |
| 2 * 2 * 15x 2 y
|
2 * 3 * 35xy 2 |
| 2 * 2 * 3 * 5 * x 2
y |
2 * 3 * 5 * 7xy 2
|
| 2 * 2 * 3 * 5 * x * x * y |
2 * 3 * 5 * 7 * x * y * y
|
| |
|
| 2 * 2 * 3 * 5
* x * x * y |
2 * 3 * 5
* 7 * x * y * y |
The underlined factors are the ones common to 60x 2
y and 210xy 2 .
Now multiply the common factors: 2 * 3 * 5 * x * y = 30xy.
The greatest common factor of 60x 2 y and 210xy
2 is 30xy.
|