Squares and Square Roots
Objective Learn the concept of square root
and how to find squares and square roots.
In this lesson, you will work with squares and square roots.
In order to find or approximate square roots, you must be
familiar with perfect squares.
Recall that the squares of a number and its opposite are
equal. That is, x 2 = ( -x ) 2.
| x |
-x |
x
2 = ( -x ) 2 |
| 0 |
0 |
0 |
| 1 |
-1 |
1 |
| 2 |
-2 |
4 |
| 3 |
-3 |
9 |
| 4 |
-4 |
16 |
| 5 |
-5 |
25 |
| 6 |
-6 |
36 |
| 7 |
-7 |
49 |
| 8 |
-8 |
64 |
| 9 |
-9 |
81 |
| 10 |
-10 |
100 |
| 11 |
-11 |
121 |
| 12 |
-12 |
144 |
Finding a square root is an inverse operation to squaring a
number.
Definition of Square Root
The square root of a number is one of its two equal factors.
In symbols, if x 2 = y , then x is a square root of y
.
Every positive number has two square roots that are opposites.
For example, 2 and -2 are square roots of 4. The number 0 only
has one square root, namely 0 itself, because 0 2 = 0,
and -0 = 0.
How many square roots does a negative number have?
None; the square of any number is positive or 0, and so no
number can have its square be a negative number. Therefore a
negative number has no square roots.
The symbol 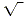 , called the radical sign , is used to
indicate a nonnegative square root. For example, , called the radical sign , is used to
indicate a nonnegative square root. For example, 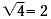 .
In particular, .
In particular, 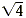 is not equal to -2. is not equal to -2.
Exercises
Write true or false. Explain your reasoning.
1. 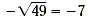 True; because True; because 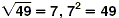 and 7 is positive. So, by taking the opposite of
both sides, we have and 7 is positive. So, by taking the opposite of
both sides, we have 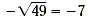 . .
2. 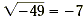 False; since -49 is negative, it has no square
roots. So, False; since -49 is negative, it has no square
roots. So, 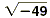 is undefined. is undefined.
The difference between Exercise 1 and Exercise 2 may be
confusing. We can take the opposite of the square root of a
positive number. However, we cannot take the square root of a
negative number. The square root of a negative number is
undefined.
So far, we have worked with numbers whose square roots are
perfect squares. When taking a square root of a number that is
not a perfect square, we need to approximate the answer. Consider
the following example.
Example
Approximate 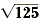 . .
Solution
Find the perfect squares closest to 125. We know that 121 = 11
2 and 144 = 12 2 . Therefore, we can conclude
that 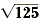 is between 11 and 12. Since 125 is closer to 121 than
to 144, we can conclude that is between 11 and 12. Since 125 is closer to 121 than
to 144, we can conclude that 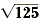 is closer to 11 than to 12. So, we can approximate
is closer to 11 than to 12. So, we can approximate 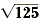 to be about 11.
to be about 11.
|