Graphing Equations in Three Variables

The graph of any equation in three variables can be drawn on a three-dimensional coordinate system. The graph of a linear equation in three variables is a plane. To solve a system of three linear equations in three variables by graphing, we would have to draw the three planes and then identify the points that lie on all three of them. This method would be difficult even when the points have simple coordinates. So we will not attempt to solve these systems by graphing.

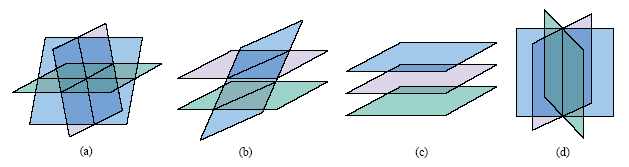
By considering how three planes might intersect, we can better understand the different types of solutions to a system of three equations in three variables. The large figure below shows some of the possibilities for the positioning of three planes in three-dimensional space. In most of the problems that we will solve the planes intersect at a single point as in figure (a). The solution set consists of one ordered triple. However, the system may include two equations corresponding to parallel planes that have no intersection. In this case the equations are said to be inconsistent. If the system has at least two inconsistent equations, then the solution set is the empty set [see figures (b) and (c)].

There are two ways in which the intersection of three planes can consist of infi- nitely many points. The intersection could be a line or a plane. To get a line, we can have either three different planes intersecting along a line, as in figure (d) or two equations for the same plane, with the third plane intersecting that plane. If all three equations are equations of the same plane, we get that plane for the intersection. We will not solve systems corresponding to all of the possible configurations described. The following examples illustrate two of these cases.