Solving Equations with Log Terms and Other
Terms
Here’s how to solve an equation that contains more than one log and a
constant term.
Procedure —
To Solve an Equation With Log Terms and Other Terms
Step 1 Rewrite the equation with the logs on one side and the
constant term on the other side.
Step 2 Combine the logs into a single log.
Step 3 Convert the equation to exponential form and solve.
Example 1
Solve: log6 x + log6 (x - 5) = 2
Solution
| Step 1 |
Rewrite the equation with the logs
on one side and the constant term
on the other side.
The logs are already on one
side of the equation.
|
log6 x + log6(x - 5) = 2 |
| Step 2 |
Combine the logs into a
single log.
Use the Log of a Product Property.
|
log6 x(x - 5)
= 2 |
| Step 3 |
Convert the equation to
exponential form and solve.
Convert to exponential form.
Simplify each side.
Subtract 36 from both sides.
Factor.
|
62 = x(x - 5)
36 = x2 - 5x
0 = x2 - 5x - 36
0 = (x - 9)(x + 4) |
| |
Use the Zero Product Property.
Solve for x. |
x - 9 = 0
x = 9 |
or
or |
x + 4
x |
= 0 = -4 |
log6 x is defined only when x is positive. Therefore, x = -4 is not a
solution.
Thus, x = 9 is the solution of log6 x + log6(x - 5)
= 2. We leave the
check to you.
Example 2
Solve: ln 20x2 = 4.73 + ln 5x.
| Step 1 |
Rewrite the equation with the logs
on one side and the constant term
on the other side.
Subtract ln 5x from both sides. |
ln 20x2
= 4.73 + ln 5x |
| Step 2 |
Combine the logs into a
single log.
|
|
| |
Use the Log of a Quotient Property. |
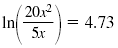 |
| |
Simplify the argument of the log.
Write ln 4x as loge 4x. |
ln 4x = 4.73 loge 4x
= 4.73 |
| Step 3 |
Convert the equation to exponential
form and solve.
Convert to exponential form. |
e4.73 = 4x |
| |
Divide both sides by 4. |
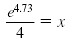 |
| |
Find e4.73 and leave the result on the
calculator display. Then, divide by 4
and round. |
28.32
≈ x |
So, x
≈ 28.32. We leave the check to you.
|