Inequalities
Some inequalities contain more information and need further
development.
Example
Solve the inequality
x - 10 < 2x - 2 < x
Solution
The method is the same as before but now there are two
inequalities to solve, i.e. x - 10 < 2x - 2 and 2x - 2 < x.
The first of these is solved in the left-hand column, the second
in the right-hand column.
Here are some examples for you to practise on.
Exercise
Find the solution to each of the following inequalities.
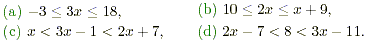
Solution
(a) Here there are two inequalities to be
solved, - 3  3 x and 3 x 18. The first of these is
- 3 3x , divide both sides by 3
- 1 x.
The second is
3x 18 , divide both sides by 3
x 6 . In both of the above inequalities the divisor is
3 , which is positive, so the division does not reverse the
inequalities.
The solution to the inequality is thus - 1 x 3.
(b) There are two inequalities here, 10 2 x and
2 x
x + 9 .
The first is
10 2 x , divide both sides by 2
5 x .
The second is
2 x x + 9 , subtract x from both sides
x 9 .
The solution to the inequality is 5 x 9 .
(c) Here there are two inequalities, x <
3x - 1 and 3x - 1 < 2x + 7. They are solved as follows.
x < 3x - 1, adding 1
x + 1< 3x, substracting x
1 < 2x, dividing by 2
1/2 < x.
3x - 1 < 2x + 7, adding 1
3x < 2x + 8, substracting 2x
x < 8.
The solution to the inequality is 1/2 < x < 8.
(d) The two inequalities in this case are 2 x
- 7 < 8 and 8 < 3x - 11. The solution to each is
2 x - 7 < 8, add 7
2x < 15, divide by 2
x < 15/2.
8 < 3x - 11, add 11
19 < 3x, divide by 3
19/3 < x.
The solution to this is 19 /3 < x < 15/2.
To end this section try the short quiz below.
Quiz
Which prime numbers satisfy the inequality.
0 2w - 3 w + 8 ?
(a) 5,7,11,13 (b) 2,5,11,17 (c) 2,3,5,7 (d) 3,7,11,13
Solution
As in previous cases there are two inequalities to be solved,
0
2 w - 3 and 2 w - 3 w + 8.
The solution to each of these is
0 2 w - 3 , add 3
3 2 w , divide by 2
3 /2 w .
2 w - 3 w + 8 , add 3
2 w w + 11 , subtract w
w 11 .
so 3 / 2 w 11. The prime numbers in this range are 2,3,5,7,11
which includes ALL those of part (c) but not all of the other
choices on offer.
|
