The Intercepts of a Parabola
A y-intercept of a function is a point where the graph crosses the y-axis.
That is, a y-intercept is a point where x = 0.
A parabola of the form f(x) = Ax2 + Bx + C always has one y-intercept.
To find it, let x = 0 in the equation and simplify:
| Quadratic Equation.
Substitute 0 for x.
Multiply.
Add. |
f(x)
f(0) |
= Ax2 + Bx + C
= A(0)2 + B(0) + C
= 0 + 0 + C
= C |
Thus, the y-intercept of f(x) = Ax2 + Bx + C is the point (0, C).
An x-intercept of a function is a point where the graph crosses the x-axis.
That is, a point where y = 0.
A parabola of the form f(x) = Ax2 + Bx + C may have 0, 1, or 2
x-intercepts.
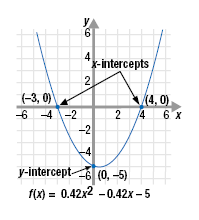
Example 1
Find the y- and x-intercepts of the function: f(x) = x2 - 3x - 10
Solution
The y-intercept is the point (0, C). Thus,
it is the point where x = 0.
| Substitute 0 for x.
Simplify. |
f(x)
f(0)
|
= x2 - 3x - 10 = (0)2
- 3(0) - 10
= -10 |
So, the y-intercept is (0, -10).
To find the x-intercepts, replace f(x) with 0 and then solve for x.
| Original function.
Substitute 0 for f(x). |
f(x)
0 |
= x2 - 3x - 10 = x2 - 3x - 10 |
To solve for x:
| Factor.
Set each factor equal to 0.
Solve each equation. |
0
x + 2
x |
= (x + 2)(x - 5) = 0 or x - 5 = 0
= -2 or x = 5 |
So, the x-intercepts of f(x) = x2 - 3x - 10 are (-2, 0) and (5, 0).
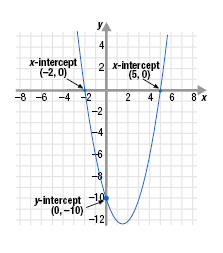
|