Exponent Laws
Summary of the exponent laws:
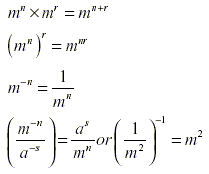
Other rules and notes
- REMEMBER THAT ONLY PARTS/CHUNKS THAT ARE MULTIPLIED OR
DIVIDED CAN BE CANCELLED.
- Things that are in brackets are considered chunks. If
there is an identical chuck then the two can be
manipulated (cancelled).
· If there are addition or subtraction between terms, then
one will need to remove those by FACTORING. Remember terms that
are added or subtracted are not covered by the exponent laws.
· If we can find a number so that the bases are the same,
then the exponents must also be the same
· If the value of two numbers is the same, and we know one
base, we know the 2 nd by default, because they must be the same
· Use a trial and error approach to solve for unknown
exponents and/or bases
Simplifying Powers
(3a 2 b)(-2a 3 b 2) = 3 ×
(-2) × a 2 × a 3 × b × b 2 =
-6 a 2 + 3 b 1 + 2 = -6a 5 b
3
Only variables which are the same can be used together. When
two variables are being multiplied we ADD their exponents.
Power of a quotient
· Reduce the quotient before you bring in the exponent.
o Same as adding exponents, but if they are in the denominator
they are subtracted.
o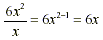
· When an exponent is to an exponent, we multiply the numbers
together
Negative Exponents
· We can clear negative exponents by taking the reciprocal
o If it is a quotient, you can subtract the negative (hence
making it positive)
Special Cases
An exponent of Zero = 1, 0 0 is not defined, there
is an understood exponent of 1 if no other number appears.
|