Rise and Run
Example 1
Find the rise and the run in moving from point P1 to point P2 on the graph.
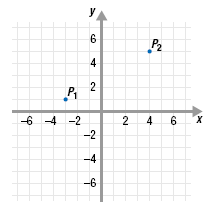
Note: In P1(x1, y1), the P stands for “point†and
the small 1 written a bit below and to the
right of P indicates point 1. The small 1 is
called a subscript. It is part of the name
for the point.
Solution
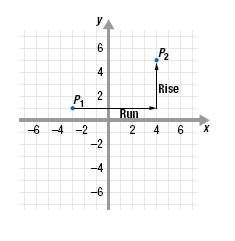
We may find the rise and the run in two ways.
Use the graph:
• To find the run, on the graph count the number of units of horizontal
change when moving from P1 to P2.
The run is 7.
• To find the rise, count the number of vertical units when moving
from P1 to P2.
The rise is 4.
Use algebra:
The coordinates of P1 are (-3, 1).
The coordinates of P2 are (4, 5).
• To find the rise, subtract the
y-coordinates. That is, find y2 - y1.
| rise |
= y2
- y1 = 5
- 1
= 4 |
Note that the y-coordinate of the
starting point, y1, is subtracted from
the y-coordinate of the ending point, y2.
• To find the run, subtract the
x-coordinates. That is, find x2 - x1.
| rise |
= x2
- x1 =
4
- (-3)
= 4 + 3 = 7 |
Example 2
a. Use the graph to find the rise and the run in moving from (-2, 1) to
(4, -3).
b. Use the graph to find the rise and the run in moving the other way, from
(4, -3) to (-2, 1).
Solution a. We are starting at (-2, 1) and moving to (4,
-3).
To find the rise, count the number of vertical units when moving
from (-2, 1) to (4, -3).
The rise is -4.
To find the run, count the number of horizontal units when moving
from (-2, 1) to (4, -3).
The run is 6.
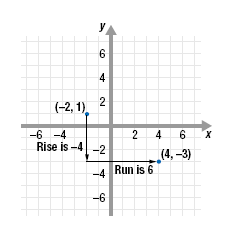
b. We are starting at (4, -3) and moving to (-2, 1).
To find the rise, count the number of vertical units when moving
from (4, -3) to (-2, 1).
The rise is 4.
To find the run, count the number of horizontal units when moving
from (4, -3) to (-2, 1).
The run is -6.
Note:
The run from (4, -3) to (-2, 1) is
-6.
This is the opposite of the run from (-2, 1) to (4,
-3).
|