Removing brackets 1

In order to simplify mathematical expressions it is frequently necessary to remove brackets. This means to rewrite an expression which includes bracketed terms in an equivalent form, but without any brackets. This operation must be carried out according to certain rules which are described in this leaflet.

1. The associativity and commutativity of multiplication

Multiplication is said to be a commutative operation. This means, for example, that 4×5 has the same value as 5×4. Eitherway the result is 20. In symbols, xy is the same as yx, and so we can interchange the order as we wish. Multiplication is also an associative operation. This means that when we want to multiply three numbers together such as 4×3×5 it doesn matter whether we evaluate 4×3 first and then multiply by 5, or evaluate 3×5 first and then multiply by 4. That is (4×3)×5 is the same as 4×(3×5) where we have used brackets to indicate which terms are multiplied first. Eitherway, the result is the same, 60. In symbols,we have (x × y) × z is the same as x × (y × z) and since the result is the same eitherway, the brackets make no difference at all and we can write simply x × y × z or simply xyz. When mixing numbers and symbols we usually write the numbers first. So

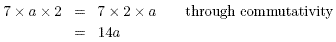
Example

Remove the brackets from

a) 4(2x)

b) a(5b)

Solution

a) 4(2x) means 4×(2 × x). Because of associativity of multiplication the brackets are unnecessary and we can write 4×2 × x

b) a(5b) means a ×(5b). Because of commutativity this is the same as (5b) × a that is (5 × b) × a. Because of associativity the brackets are unnecessary and we write simply 5 × b × a which equals 5ba. Note that this is also equal to 5ab because of commutativity.

Exercises

1. Simplify

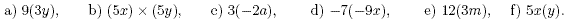
Answers

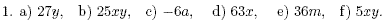
2. Expressions of the form a( b + c ) and a( b - c )

Study the expression 4×(2 + 3).

By working out the bracketed term first we obtain 4×5 which equals 20. Note that this is the same as multiplying both the 2 and 3 separately by 4, and then adding the results. That is 4×(2 + 3) = 4×2 + 4×3 = 8 + 12 = 20.

Note the way in which the "4" multiplies both the bracketed numbers, "2" and "3". We say that the "4" distributes itself over both the added terms in the brackets - multiplication is distributive over addition.

Now study the expression 6×(8 - 3).

By working out the bracketed term first we obtain 6×5 which equals 30. Note that this is the same as multiplying both the 8 and the 3 by 6 before carrying out the subtraction:

6×(8 - 3) = 6×8 -6×3 = 48 - 18 = 30.

Note the way in which the "6" multiplies both the bracketed numbers. We say that the "6" distributes itself over both the terms in the brackets - multiplication is distributive over subtraction. Exactly the same property holds when we deal with symbols.

a (b + c) = ab + ac

a (b - c) = ab - bc

Example

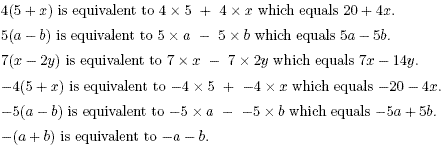
Exercises

Remove the brackets from each of the following expressions simplifying your answers where appropriate.

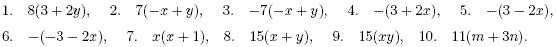
Answers
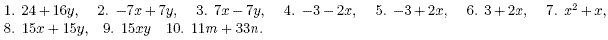