Quadratic Expressions
Complete Squares
Look at the following quadratic expression:
x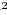 - 4x + 4 = (x - 2)(x - 2) = (x - 2) - 4x + 4 = (x - 2)(x - 2) = (x - 2)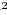 . .
For the obvious reason, this expression is called a complete
square. Quadratic expressions which can be factored into
a complete square are useful in many situations. They have a
particularly simple structure and it is important to be able to
recognise such factorizations.
Example 3
Show that the following quadratic expressions are complete
squares.
(a) x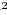 + 6 x + 9 , (b) x + 6 x + 9 , (b) x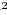 + 4 x + 4 , (c) x + 4 x + 4 , (c) x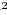 - 2 x + 1 , (d) x - 2 x + 1 , (d) x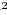 - 2 ax + a 2 . - 2 ax + a 2 .
Solution
In each of these cases it is easy to check the following.
(a) x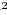 + 6 x + 9 = ( x + 3) + 6 x + 9 = ( x + 3)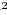 , ,
(b) x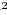 + 4 x + 4 = ( x + 2) + 4 x + 4 = ( x + 2)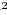 , ,
(c) x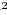 - 2 x + 1 = ( x - 1) - 2 x + 1 = ( x - 1)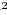 , ,
(d) x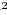 - 2 ax + a - 2 ax + a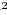 = ( x - a) = ( x - a)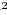 . .
The last example, x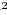 - 2ax + a - 2ax + a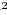 = (x - a) = (x - a)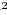 , is a general case and it may be used to
find perfect squares for any given example. It may be usefully
employed in finding solutions to the following exercises. , is a general case and it may be used to
find perfect squares for any given example. It may be usefully
employed in finding solutions to the following exercises.
|