Adding Fractions with Unlike Denominators
Objective To learn how to add and subtract
fractions with unlike denominators, using the method of common
denominators.
This lesson contains the most complicated operations on
fractions.
Using Models to Add Fractions with Unlike Denominators
When adding fractions with unlike denominators, we cannot just
add the numerators the way we do when the fractions have like
denominators.
Example 1
What is 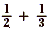 ? ?
Solution
In order to find this sum, we first need to rewrite both
fractions so they have the same denominator. This means we must
replace each fraction with an equivalent fraction having a
different denominator.
First, let's draw a separate model for each of the fractions.
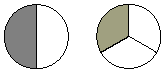
The addition is modeled by taking the two parts together as a
portion of a whole pizza.
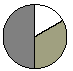
It is not easy to visually determine what fraction of the
whole pizza is represented by the shaded portion of the model.
However, suppose we divided each pizza into 2 × 3 or 6 equal
parts.
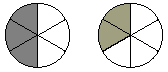
Notice that each of the smaller parts we have created is one
sixth of the pizza. Now when we merge the portions of the pizza,
we get the model below.
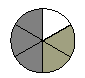
We can see that the shaded portion of the model consists of
five pieces, each of which is one sixth of the pizza. In other
words, the shaded portion of the pizza represents the fraction 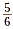 , so , so 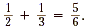
Example 2
What is 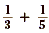 ? ?
Solution
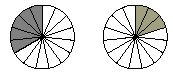
Represent each of the fractions 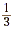 and and 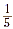 as portions of a pizza. as portions of a pizza.
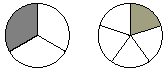
When we merge these two portions, we get this picture.
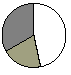
To determine what fraction is modeled by the combined shaded
regions in the figure above, divide each pizza into 3 × 5 or 15
equal parts.
Each of the smaller parts we have created represents one
fifteenth of the pizza. The merged version of these portions is
shown below.
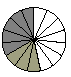
The shaded portion of the model above consists of eight
pieces, each of which is one fifteenth of the pizza. The shaded
portion of the model represents 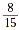 , so , so 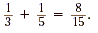
|