Extraneous Roots
Because equations involving rational expressions have variables in denominators, a
root to the equation might cause a 0 to appear in a denominator. In this case the root
does not satisfy the original equation, and so it is called an extraneous root.
Example 1
An equation with an extraneous root
Solve
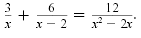
Solution
Because x2 - 2x = x(x - 2), the LCD for x, x - 2, and x2
- 2x is x(x - 2).
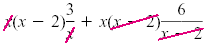 |
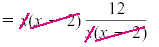 |
Multiply each side by x(x - 2). |
| 3(x - 2) + 6x 3x - 6 + 6x
9x - 6
9x
x |
= 12
= 12
= 12
= 18
= 2 |
|
Neither 0 nor 2 could be a solution because replacing x by either 0 or 2 would cause
0 to appear in a denominator in the original equation. So 2 is an extraneous root and
the solution set is the empty set, Ø.
Example 2
An equation with an extraneous root
Solve
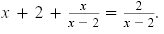
Solution
Because the LCD is x - 2, we multiply each side by x - 2:
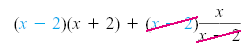 |
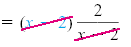 |
| x2 - 4 +
x |
= 2 |
| x2 + x -
6 |
= 0 |
| (x + 3)(x - 2) |
= 0 |
| x + 3 = 0 |
or |
x - 2 |
= 0 |
| x = -3 |
or |
x |
= 2 |
Replacing x by 2 in the original equation would cause 0 to appear in a denominator.
So 2 is an extraneous root. Check that the original equation is satisfied if x =
-3. The solution set is {-3}.
|