Solving Equations
We are now ready to move on to slightly more sophisticated
examples.
Example
Find the solution to the equation
5( x - 3) - 7(6 - x ) = 24 - 3(8 - x ) - 3
Solution
Removing the brackets from both sides first and then
simplifying:
5( x - 3) - 7(6 - x ) = 24 - 3(8 - x ) - 3
5 x - 15 - 42 + 7 x = 24 - 24 + 3 x - 3
5 x + 7 x - 15 - 42 = 3 x - 3
12 x - 57 = 3 x - 3 .
Adding 57 to both sides:
12x = 3x - 3 + 57 = 3x + 54
Subtracting 3x from both sides:
12x - 3x = 54 o r 9x = 54 giving x = 6 .
Exercise
Find the solution to each of the following equations.
(a) 2 x + 3 = 16 - (2 x - 3)
(b) 8( x - 1) + 17( x - 3) = 4(4 x - 9) + 4
(c) 15( x - 1) + 4( x + 3) = 2(7 + x )
Solutions
(a) 2 x + 3 = 16 - (2 x - 3) = 16 - 2 x + 3 =
19 - 2 x
Now add 2x to both sides and subtract 3 from both sides
2 x + 3 = 19 - 2 x
4 x + 3 = 19
4 x = 19 - 3
4 x = 16
and the solution is x = 4 . This can be checked by putting x =
4 in both sides of the first equation above and noting that each
side will have the value 11.
(b)
8( x - 1) + 17( x - 3) = 4(4 x - 9) + 4
8 x - 8 + 17 x - 51 = 16 x - 36 + 4
25 x - 59 = 16 x - 32
25 x - 16 x - 59 = - 32
9 x - 59 = - 32
9 x = 59 - 32
9 x = 27
x = 3 .
Inserting x = 3 into the equation we can check that both sides
have the value 16.
(c)
15( x - 1) + 4( x + 3) = 2(7 + x )
15 x - 15 + 4 x + 12 = 14 + 2 x
19 x - 3 = 2 x + 14
19 x - 2 x - 3 = 14
17 x - 3 = 14
17 x = 14 + 3 = 17
x = 1
Inserting x = 1 into the equation we can check that both sides
have the value 16.
Quiz
Which of the following is the solution to the equation
5x - (4x - 7)(3x - 5) = 6 - 3(4x - 9)(x - 1) ?
(a) - 2 (b) - 1 (c) 2 (d) 4
Solution:
First expand the brackets separately using FOIL (see the
package on Brackets ):
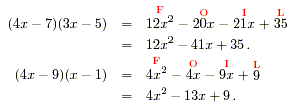
These can now be substituted, carefully, into the equation:
5 x - [ (4 x - 7)(3 x - 5) ] = 6 - 3 [ (4 x - 9)( x - 1) ]
5 x - [ 12 x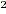 - 41 x + 35 ] = 6 - [ 4 x - 41 x + 35 ] = 6 - [ 4 x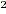 -
13 x + 9 ] -
13 x + 9 ]
5 x - 12 x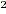 + 41 x - 35 = 6 - 4 x + 41 x - 35 = 6 - 4 x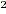 +
13 x - 9 +
13 x - 9
- 12 x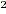 + 46 x - 35 = - 12 x + 46 x - 35 = - 12 x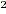 +
39 x - 21 . +
39 x - 21 .
Notice the extra pair of square brackets in the first equation
above. These are to emphasise that the negative sign multiplies
all of the parts inside the [ ] brackets. The procedure now
follows in an obvious manner. Add 12 x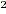 to
both sides, subtract 39 x from both sides then add 35 to both
sides: to
both sides, subtract 39 x from both sides then add 35 to both
sides:
- 12 x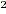 + 46 x - 35 = - 12 x + 46 x - 35 = - 12 x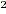 +
39 x - 21 +
39 x - 21
46 x - 35 = 39 x - 21
46 x - 39 x - 35 = - 21
46 x - 39 x = 35 - 21
7 x = 14
x = 2 .
|