Quadratic Equations
Example
The solutions of a quadratic equation are 5 and
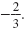
Work backwards to find a quadratic equation with these solutions.
Solution
| Begin by writing the two solutions.
|
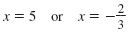 |
| To clear the fraction in the second
solution, multiply both sides of the
second equation by 3.
|
x = 5 or 3x = -2 |
| Move the constant to the left side of
each equation. |
x - 5 = 0 or 3x + 2 = 0 |
| Since each binomial is equal to 0,
their product is 0. |
(x - 5)(3x + 2) = 0 |
| Multiply the binomials.
Combine like terms. |
3x2 + 2x - 15x - 10 = 0
3x2 - 13x - 10 = 0 |
The quadratic equation 3x2 - 13x - 10 = 0
has the given solutions, 5 and
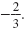
Note:
3x2 - 13x - 10 = 0
Any nonzero multiple of this equation
also has solutions 5 and
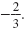
Here are some examples:
6x2 - 26x - 20 = 0
15x2 - 65x - 50 = 0
The quadratic formula states that the solutions of a quadratic equation,
ax2 + bx + c = 0, are
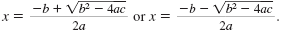
Let’s see what happens when we combine the solutions first by addition
and then by multiplication:
| • When we add the solutions,
the radicals are eliminated.
|
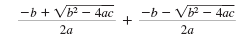 |
| Add the numerators to
form one fraction. |
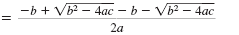 |
| Combine like terms. The
square root terms add to
zero. |
 |
| Cancel the common
factor, 2. |
 |
Thus, for a quadratic equation, ax2 + bx + c = 0, the sum of the solutions
is
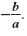
• When we multiply the solutions, the radicals are eliminated.
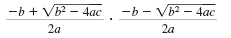
Multiply the numerators and multiply the denominators.
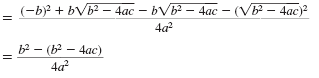
Combine like terms.
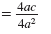
Cancel the common factor, 4a.
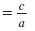
Thus, for a quadratic equation, ax2 + bx + c = 0, the product of the solutions is
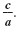
|