Scientific Notation vs Standard Notation
Converting from Scientific Notation to Standard Notation
Many of the numbers occurring in science are either very large or very small.
The speed of light is 983,536,000 feet per second. One millimeter is equal to
0.000001 kilometer. In scientific notation, numbers larger than 10 or smaller
than 1 are written by using positive or negative exponents.
Scientific notation is based on multiplication by integral powers of 10.
Multiplying a number by a positive power of 10 moves the decimal point to the
right:
| 10(5.32) 102(5.32)
103(5.32) |
= 53.2 = 100(5.32) = 532
= 1000(5.32) = 5320 |
Multiplying by a negative power of 10 moves the decimal point to the left:
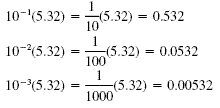
So if n is a positive integer, multiplying by 10 n moves the
decimal point n places to the right and multiplying by 10 -n moves
it n to the left.
A number in scientific notation is written as a product of a number between
1 and 10 and a power of 10. The times symbol × indicates multiplication. For
example, 3.27 × 109 and 2.5 × 10 -4 are numbers in
scientific notation. In scientific notation there is one digit to the left of
the decimal point.
To convert 3.27 × 109 to standard notation, move the decimal
point nine places to the right:
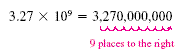
In general, we use the following strategy to convert from scientific
notation to standard notation.
Strategy for Converting from Scientific Notation to Standard Notation
1. Determine the number of places to move the decimal point by examining
the exponent on the 10.
2. Move to the right for a positive exponent and to the left for a negative
exponent.
Example
Converting scientific notation to standard notation
Write in standard notation.
a) 7.02 × 106
b) 8.13 × 10 -5
Solution
a) Because the exponent is positive, move the decimal point six places to
the right:
7.02 × 106 = 7020000 = 7,020,000
b) Because the exponent is negative, move the decimal point five places to
the left.
b) 8.13 × 10 -5 = 0.0000813
Converting from Standard Notation to Scientific Notation
To convert a positive number to scientific notation, we just reverse the
strategy for converting from scientific notation.
Strategy for Converting to Scientific Notation
1. Count the number of places (n) that the decimal must be moved so that it
will follow the first nonzero digit of the number.
2. If the original number was larger than 10, use 10n.
3. If the original number was smaller than 10, use 10 -n.
Remember that the scientific notation for a number larger than 10 will have a
positive power of 10 and the scientific notation for a number between 0 and 1
will have a negative power of 10.
Example 2
Converting numbers to scientific notation
Write in scientific notation.
a) 7,346,200
b) 0.0000348
c) 135 × 10 -12
Solution
a) Because 7,346,200 is larger than 10, the exponent on the 10 will be
positive:
7,346,200 = 1.3462 × 106
b) Because 0.0000348 is smaller than 1, the exponent on the 10 will be
negative:
0.0000348 = 3.48 × 10 -5
c) There should be only one nonzero digit to the left of the decimal point:
| 135 × 10 -12 |
= 1.35 × 10 2 × 10 -12 |
Convert 135 to scientific notation. |
| |
= 1.35 × 10 -10 |
Product rule |
|