Polynomial Equations
Solving a Quadratic Inequality
Solve the quadratic inequality:
12· x2 - 22 · x
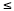 4. 4.
Solution
The graphs of the quadratic (
y =12 · x2 - 22· x) and the horizontal line ( y = 4) are shown
together in the graph below. As we are looking for the x-values that make the height of
the quadratic less than the height of the horizontal line, our answer will consist of all xvalues
that lie between the two intersection points (including the intersection points
themselves as the “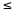 †sign is used, rather than the “<†sign.) †sign is used, rather than the “<†sign.)
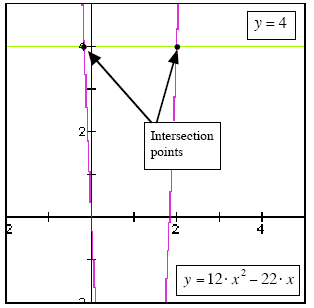
To locate the x-coordinates of the points where the quadratic and the horizontal line meet,
we must manipulate the given inequality to make the right hand side of the inequality
equal to zero. To do this we can subtract 4 from both sides.
12 · x2 - 22 · x - 4
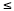 0. (Subtract 4 from both sides) 0. (Subtract 4 from both sides)
To find the x-coordinates of the intersection points, you need to solve the quadratic
equation:
12 · x2 - 22 · x - 4 = 0.
Solving this quadratic equation with the quadratic formula gives:
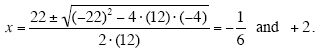
So, the solution to the quadratic inequality consists of the intervals of x-values:
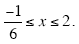
Polynomial Equations
A polynomial equation is an equation of the form:
y = c0 + c1·x + c2·x2 + ... + cn·xn
where the powers of x must be positive integers. The letters c0, c1, … , cn represent
numbers.
The largest power of x in the polynomial is called the degree of the polynomial.
Polynomial Functions that You Already Know About
Each of the different types of polynomial functions has a distinctively shaped graph.
Some of the polynomials (and shapes) that you are already familiar with include:
Degree 0 polynomials (i.e. constant functions) have graphs that are horizontal lines.
Degree 1 polynomials (i.e. linear functions) have graphs that are straight lines.
Degree 2 polynomials (i.e. quadratic functions) have graphs that are
parabolas.
Degree 3 polynomials (called cubics) have graphs that look like John Travolta from the
cover of the Saturday Night Fever movie soundtrack (see Figure 1).
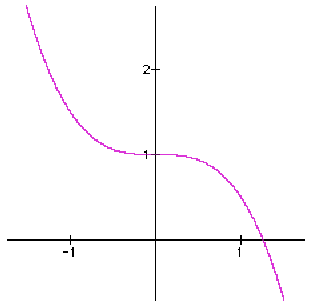
Figure 1: The graph of a polynomial function of degree 3.
|