Powers and Exponents

Objective

Learn the idea of exponentiation and the notion of raising a number to a power.

Exponential notation is very important in all future uses of mathematics.

Raising Numbers to a Power

Remember that the area of a rectangle is the product of the lengths of the sides. When the rectangle is a square, we can find the area by multiplying one side times itself. In the same way, the volume of a cube is found by multiplying one side times itself three times.

The idea of multiplying a number repeatedly by itself comes up so often that a special notation has been invented for it.

Notation

We will write x ⁿ for the result of multiplying n "repeats" of x together. The number x is called the base, and the number n is called the exponent.

For instance,

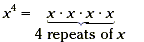	base = x, exponent = 4
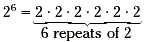	base = 2, exponent = 6
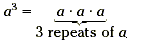	base = a, exponent = 3

For the expression x ², we say x squared. For the expression x ³, we say x cubed. Otherwise, for x ⁿ, we say x raised to the nth power. For example, 5 raised to the 4th power is written 5 ⁴, and a raised to the fourth power is written a ⁴. Note that the exponent can be 1. For example, x ¹ = x . A power of a number a is a number found by raising a to a power.

Let's see some examples of expanding powers into products and raising numbers to exponents.

Example 1

Write 3 ⁵ , x ⁷ , a ⁴ , and b ⁸ as products.

Solution

3 ⁵ = 3 · 3 · 3 · 3 · 3

x ⁷ = x · x · x · x · x · x · x

a ⁴ = a · a · a · a

b ⁸ = b · b · b · b · b · b · b · b

Example 2

Write 4 · 4 · 4, d · d · d · d · d · d , and ( z + y ) · ( z + y ) using exponents.

Solution

4 · 4 · 4 = 4 ³

d · d · d · d · d · d = d ⁶

( z + y ) · ( z + y ) = ( z + y ) ²

Now is a good time to explain the roles of the powers of ten in our place-value system. That is, every number can be written as a sum of single-digit number times a power of ten. When the powers of ten are written explicitly, we call the expression the expanded form of the number. The expanded form of 1234 is shown below. Notice that 1 = 10 ⁰. Any number raised to the zero power equals 1.

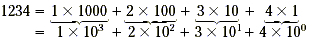
We have introduced the idea of exponentiation. Now, it is important to extend the rules for order of operations to include exponents.

Definition of Order of Operations

1. Do all operations within parentheses first; start with an innermost pai r of parentheses.

2. Evaluate all powers in order from left to right.

3. Perform all multiplications and divisions in order from left toright.

4. Perform all additions and subtractions in order from left to right.

Here are some examples to illustrate this idea.

Example 3

Evaluate ab ² if a = 2 and b = 3.

Solution

Notice that we evaluated the power before the product. If we hadn't done this, we would have multiplied first to get 6 ² or 36.

Example 4

Evaluate (2 + 4 ² ) (9 ² + 3 · 4).

Solution

Notice the order of operations. If the operations were performed in any other order, we would have arrived at a different, incorrect answer.