Solving Quadratic Equations
Factorizing a quadratic expression and finding the roots of a
quadraticequation are closely related.
Example 1
Find the solution to the equations
(a) x + 6cx + 8 = 0, (b) x - 4x + 4 = 0.
Solution
(a) The quadratic expression will factorize as follows.
x + 6x + 8 = (x + 2)(x + 4).
The solution to the equation may now be obtained;
If x + 6x + 8 = 0
then (x + 2)(x + 4) = 0 .
Thus either (x + 2) = 0, or (x + 4) = 0. The solution to the
equation is thus x = -2 or x = -4.
(b) In this example the expression is
x - 4x + 4 = (x - 2)(x - 2) = (x - 2) .
The solution to the equation x - 4x + 4 = 0 is thus x = 2.
In this case, the equation is said to have equal roots.
Exercise 1
Find the solution to each of the following equations.
(a) 2x + 5x + 3 = 0
(b) 3x + 7x + 2 = 0
(c) 3y - 5y - 2 = 0
(d) 4z - 23z + 15 = 0
(e) 64z + 4z - 3 = 0
(f) 4w - 25 = 0
Solution
(a) We can easily see that
2x + 5x + 3 = (2x + 3)(x + 1) .
Thus if 2x + 5x + 3 = 0 then we have
either (2x + 3) = 0 , or (x + 1) = 0.
For the first of these
2x + 3 = 0
2x = -3 (adding -3 to both sides)
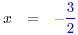 (dividing both sides by 2) .
The solution to the second is obviously x = -1.
(b) We can easily see that
3x + 7x + 2 = (3x + 1)(x + 2) ,
so that if 3x + 7x + 2 = 0 ,
then (3x + 1)(x + 2) = 0 .
Thus either 3x + 1 = 0 or x + 2 = 0 .
For the first of these 3x + 1 = 0
3x = -1 (adding -1 to both sides)
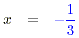 (dividing both sides by 3) .
The solution to the second part is obviously x = -2. The
solution to the original equation is thus x = -2 or x = -1/3.
(c) We can easily see that
3y - 5y - 2 = (3y + 1)(y - 2) = 0 .
Thus either 3y + 1 = 0, or y - 2 = 0. For the first part,
3y + 1 = 0 ,
3y = -1 (adding -1 to both sides) ,
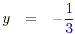 (dividing both sides by 3) .
The solution to the second part is obviously y = 2.
The quadratic equation 3y - 5y - 2 = 0 thus has the solution y = -1/3 or y =
2.
(d) We can easily see that
4z - 23z + 15 = (4z - 3)(z - 5) = 0 .
Thus either 4z - 3 = 0, or z - 5 = 0.
Proceeding as in the previous examples, the solution to the
first partis z = 3/4 and to the second part is z = 3.
The solution to 4z - 23z + 15 = 0 is therefore z = 3/4 or z = 3.
(e) We can easily see that
64z + 4z - 3 = (16z - 3)(4z + 1) = 0 .
Thus either 16z - 3 = 0 or 4z + 1 = 0. For the first part
16z - 3 = 0 ,
16z = 3 (adding 3 to both sides) ,
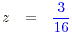 (dividing both sides by 16) .
For the second part 4z + 1 = 0
4z = -1 (adding -1 to both sides) ,
z = -14 (dividing both sides by 4) .
The solution to the equation 64z + 4z - 3 = 0 is thus z = 3/16 or z = -1/4.
(f) We can easily see that
4w - 25 = (2w - 5)(2w + 5) = 0.
The solution to this is w = 5/2 or w = -5/2 , i.e. w = ±5/2 .
Quiz
Which of the following is the solution to the quadratic
equation 12x + 17x - 14 = 0 ?
(a) 2, 7/12 (b) -2, -7/12 (c) -2, 7/12 (d) 2, -7/12
Solution
This quadratic is the one that occurs in the first quiz. There
it was seen that 12x + 17x - 14 = (x + 2)(12x - 7), so
either x + 2 = 0 or 12x - 7 = 0 .
The solution to the first is x = -2 and to the second is x =
7/12.
|
