Powers and roots
Introduction
Powers are used when we want to multiply a number by itself
repeatedly.
1. Powers
When we wish to multiply a number by itself we use powers, or
indices as they are also called. For example, the quantity 7×
7×7×7 is usually written as 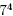 . The
number 4 tells us the number of sevens to be multiplied together.
In this example, the power, or index, is 4. The number 7 is
called the base. . The
number 4 tells us the number of sevens to be multiplied together.
In this example, the power, or index, is 4. The number 7 is
called the base.
Example
6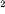 = 6×6 = 36. We say that "6 squared is 36", or "6
to the power 2 is 36".
= 6×6 = 36. We say that "6 squared is 36", or "6
to the power 2 is 36".
2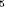 = 2×2×2×2×2. We say that "2 to the power 5 is 32".
= 2×2×2×2×2. We say that "2 to the power 5 is 32".
Your calculator will be pre-programmed to evaluate powers.
Most calculators have a button marked  , or
simply ^. Ensure that you are using your calculator correctly by
verifying that 3 , or
simply ^. Ensure that you are using your calculator correctly by
verifying that 3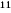 = 177147. = 177147.
2. Square roots
When 5 is squared we obtain 25. That is 5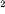 = 25. = 25.
The reverse of this process is called finding a square root.
The square root of 25 is 5. This is written as 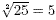 , or
simply , or
simply 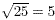 . .
Note also that when -5 is squared we again obtain 25, that is
(-5)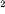 = 25. This means that 25 has another square root, -5.
= 25. This means that 25 has another square root, -5.
In general, a square root of a number is a number which when
squared gives the original number. There are always two square
roots of any positive number, one positive and one negative.
However, negative numbers do not possess any square roots.
Most calculators have a square root button, probably marked  . Check
that you can use your calculator correctly by verifying that . Check
that you can use your calculator correctly by verifying that 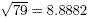 , to
four decimal places. Your calculator will only give the positive
square root but you should be aware that the second, negative
square root is -8.8882. , to
four decimal places. Your calculator will only give the positive
square root but you should be aware that the second, negative
square root is -8.8882.
An important result is that the square root of a product of
two numbers is equal to the product of the square roots of the
two numbers. For example
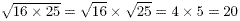
More generally,
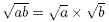
However your attention is drawn to a common error which
students make. It is not true that 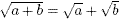 .
Substitute some simple values for yourself to see that this
cannot be right. .
Substitute some simple values for yourself to see that this
cannot be right.
Exercises
1. Without using a calculator write down the value of 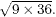
Find the square of the following: 
3. Show that the square of 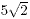 is
50. is
50.
Answers
1. 18, (and also -18).
2. a) 2, b) 12.
3. Cube roots and higher roots
The cube root of a number, is the number which when cubed
gives the original number. For example, because 4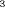 = 64 = 64
we know that the cube root of 64 is 4, written 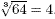 All
numbers, both positive and negative, possess a single cube root. All
numbers, both positive and negative, possess a single cube root.
Higher roots are defined in a similar way: because 2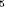 = 32,
the fifth root of 32 is 2, written = 32,
the fifth root of 32 is 2, written 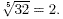
Exercises
1. Without using a calculator find 
Answers
1. a) 3, b) 5.
Surds
Expressions involving roots, for example  and and 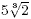 are
also known as surds. Frequently, in engineering calculations it
is quite acceptable to leave an answer in surd form rather than
calculatingits decimal approximation with a calculator. are
also known as surds. Frequently, in engineering calculations it
is quite acceptable to leave an answer in surd form rather than
calculatingits decimal approximation with a calculator.
It is often possible to write surds in equivalent forms. For
example, 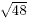 can be written as can be written as 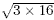 , that
is , that
is 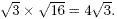
Exercises
1. Write the following in their simplest surd form: 
2. By multiplying numerator and denominator by 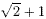 , show
that , show
that

Answers
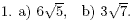
|