Undefined Rational Expressions
Determining When a Rational Expression is
Undefined
A rational number is a number that can be written in the form
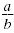 where a and b are integers and b
≠ 0. where a and b are integers and b
≠ 0.
For example,
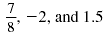 are rational numbers.
are rational numbers.
We define a rational expression in a similar manner.
Definition —
Rational Expression
A rational expression is an expression that can be written in the
form
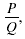 where P and Q are polynomials and Q
≠ 0. where P and Q are polynomials and Q
≠ 0.
Note:
The integer -2 is a rational number, since
it can be written as
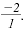 Likewise, 1.5 is a rational number, since it
can be written as Likewise, 1.5 is a rational number, since it
can be written as
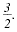
Remember, constants such as 2 and 7 are
monomials of degree 0. So,
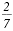 is an example of a rational
expression. is an example of a rational
expression.
Here are some examples of rational expressions:

The denominator of a rational expression cannot equal 0. This is because
division by 0 is undefined. Therefore, it is important to determine the
values of the variable that make the denominator 0. We say that the
rational expression is undefined for those values.
Example 1
Find the value(s) of x for which this
rational expression is undefined:
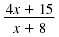
Solution
The rational expression is undefined when its denominator is 0.
| Set the denominator equal to 0.
Then solve for x.
Subtract 8 from both sides.
|
x + 8 = 0
x = -8 |
| When x = -8, the denominator is 0.
|
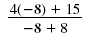 |
| We have |
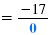 |
Therefore,
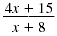 is undefined when x
= -8. is undefined when x
= -8.
Note:
It’s okay for the numerator of a rational
expression to equal 0.
For example,
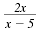 is defined when x
= 0. is defined when x
= 0.
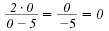
However,
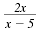 is not defined when x
= 5. is not defined when x
= 5.
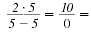 undefined undefined
Example 2
Find the value(s) of x for which this
rational expression is undefined:
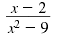
Solution
| Set the denominator equal to zero.
Then solve for x.
Factor the left side of the equation.
Use the Zero Product Property.
Solve these equations. |
x2 - 9
(x - 3)(x + 3)
x - 3 = 0
x =3 |
= 0
= 0
or
or |
x + 3 = 0
x = -3 |
Therefore,
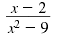 is undefined when x
= 3 or x = -3. is undefined when x
= 3 or x = -3.
|