Finding the Greatest Common Factor (GCF)
After studying this lesson, you will be able to:
- Find the prime factorization of an integer.
- Find the GCF for a set of monomials.
Prime numbers are those numbers greater than
one whose only factors are one and itself. A partial list of
prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...
One way to find a prime factorization of an integer is to use
"factor trees".
Example 1
Find the prime factorization of 15
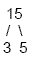
Factor the number down until all you have left is prime
numbers
Write the prime factorization: 3 · 5
Example 2
Find the prime factorization of 30
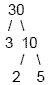
Factor the number down until all you have left is prime
numbers
Write the prime factorization: 2 · 3 · 5
Example 3
Find the prime factorization of -525
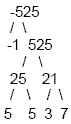
Factor out the negative to begin with
Write the prime factorization: -1 · 3 · 5 2· 7
Example 4
Find the prime factorization of 20a 2 b
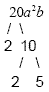
Don't worry about the variables until the last step.
Write the prime factorization: 2 2 · 5 · a · a
· b (we factored the variables, too)
Example 5
Find the prime factorization of 60a 2 b 2
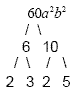
Don't worry about the variables until the last step.
Write the prime factorization: 2 2 · 3 · 5 · a
· a · b · b
Greatest Common Factors
Sometimes we need to be able to find the greatest common
factor of a set of numbers. The greatest common, or GCF, is the
largest number that will divide evenly into each of the numbers
in a set.
Example 6
Find the GCF for the set of numbers: 10, 12, 20
The largest number that will go into each of these numbers is
2.
Example 7
Find the GCF for the set of numbers: 6, 18, 36
The largest number that will go into each of these numbers is
6.
Example 8
Find the GCF for the set of numbers: 4, 8, 10
The largest number that will go into each of these numbers is
2.
Example 9
Find the GCF for the set of numbers: 8a 2 b, 18a 2
b 2 c
The first thing we do is find the GCF for the coefficients -
just like we've been doing. The largest number that will go into
each of the coefficients is 2.
Since we have variables, we have to find their GCF also. For a
variable to be included in the GCF, each term must have the
variable. If the variable is in each term, we take the lowest
exponent of the variable and include it in the GCF.
In this case, both terms have a and both terms have b . We
will include a 2 because that is the lowest power of a
. We will include b because that is the lowest power of b .
The GCF will be 2 a 2 b
Example 10
Find the GCF for the set of numbers: 3x 2 y, 12x 4
y 2, 9x 2 y
The first thing we do is find the GCF for the coefficients.
The largest number that will go into each of the coefficients is
3.
Since we have variables, we have to find their GCF also. For a
variable to be included in the GCF, each term must have the
variable. If the variable is in each term, we take the lowest
exponent of the variable and include it in the GCF.
In this case, both terms have x and both terms have y . We
will include x 2 because that is the lowest power of x
. We will include y because that is the lowest power of y .
The GCF will be 3x 2 y
|