Adding and Subtracting Rational Expressions with Different Denominators
In the next example we must first factor polynomials to find the LCD.
Example 1
Different denominators
Perform the indicated operations.

Solution
a) Because x2 - 1 = (x + 1)(x + 1) and x2 + x = x(x + 1), the LCD is
x(x - 1)(x + 1). The first denominator is missing the factor x, and the second
denominator is missing the factor x - 1.
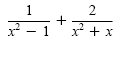 |
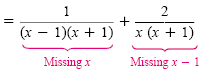 |
The LCD is
x(x - 1)(x + 1). |
| |
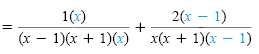 |
Build up the
denominators to
the LCD. |
| |
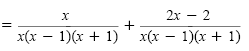 |
|
| |
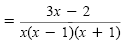 |
Add the
numerators.
|
For this type of answer we usually leave the denominator in factored form. That
way, if we need to work with the expression further, we do not have to factor the
denominator again.
b) Because -1(2 - a) = a - 2, we can convert the denominator 2 - a to a - 2.
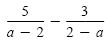 |
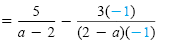 |
|
| |
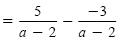 |
The LCD is a - 2. |
| |
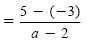 |
Subtract the numerators. |
| |
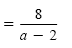 |
Simplify. |
Note that if we had changed the denominator of the first expression to 2 - a, we
would have gotten the answer
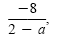
but this rational expression is equivalent to the first answer.
Helpful hint
It is not actually necessary to
identify the LCD. Once the denominators
are factored, simply
look at each denominator
and ask,“What factor does the
other denominator have that
is missing from this one?â€
Then use the missing factor to
build up the denominator and
you will obtain the LCD.
|