Adding and Subtracting Fractions
Finding “Lowest Common Denominators”
Before two fractions can be added, they may have to be
converted to equivalent fractions so that both have the same
denominator, a so-called common denominator. Let's describe this
process.
When attempting a sum such as
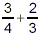
we need to first convert both fractions to equivalent
fractions which have the same denominator. The method for
obtaining equivalent fractions is to multiply the numerator and
denominator of the given fraction by the same number:
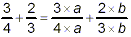
where ‘a’ and ‘b’ stand for some whole
numbers which have values so that
4a = 3b = LCD
Actually, any values of ‘a’ and ‘b’ that
satisfy this condition will work, but there are advantages to
picking ‘a’ and ‘b’ so that the resulting
number, LCD, is as small as possible. Since this smallest number
will be the new denominator for both fractions, it is called the lowest
common denominator or LCD.
From the condition above, we see that LCD = 4a, so LCD must be
evenly divisible by 4 (since ‘a’ is supposed to be a
whole number). Similarly, LCD = 3b, so LCD must be divisible by 3
(since ‘b’ is supposed to be a whole number).
The systematic procedure for finding LCD in this case is as
follows:
step (i): write each of the original
denominators as a product of prime factors: Here:
4 = 2 2
3 = 3
a very simple situation.
step (ii): A power of every distinct prime
factor that occurs in any of the denominators will be a factor of
the LCD.
Here:
LCD = 2 x · 3 y
since the only distinct prime factors in the original
denominators are 2 and 3 in this case.
step (iii): The powers of each factor in the
LCD are just the highest power to which that factor is raised in
any of the original denominators.
So here,
x = 2, since 4 contains 2 2 and 3 contains 2 0.
Therefore, the highest power of 2 that occurs in either of the
original denominators is 2.
y = 1, since 4 contains 3 0 and 3 contains 3 1.
Therefore the highest power of 3 occurring in either of the
original denominators is 1.
Thus, for this simple example,
LCD = 2 2 · 3 = 12
(This happens to be equal to the product, 4 × 3, of the
original denominators in this case. However, often the LCD is
much smaller than the product of the original denominators
because of common prime factors between them. The fact that the
LCD can be smaller or simpler than the product of the original
denominators is why this procedure for finding the LCD is
worthwhile. Using the LCD is particularly important when working
with algebraic fractions.)
step (iv): Convert the original fractions to
equivalent fractions with this LCD as denominator and do the
arithmetic. The numbers ‘a’ and ‘b’ involved
in this conversion, as illustrated above, are just LCD divided by
the original denominators of each fraction.
So, in our simple example, the fraction 3 / 4 must be
multiplied top and bottom by
LCD / 4 = 12 / 4 = 3, and the fraction 2 / 3 must be
multiplied top and bottom by
LCD / 3 = 12 / 3 = 4:
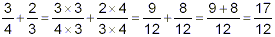
Sometimes people write this conversion to equivalent fractions
as multiplication by fractions with identical numerators and
denominators, as in:
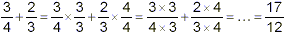
but because of the rule for multiplication of fractions, the
result is the same.
|