Brackets
Quantities are enclosed within brackets to indicate that they
are to be treated as a single entity. If we wish to subtract,
say, 3a - 2b from 4a - 5b then we do this as follows.
Example 1
(a)
| (4a - 5b ) -
(3a - 2b ) |
= 4a - 5b - 3a - ( -2b ) =
4a - 5b - 3a + 2b
= 4a - 3a - 5b + 2b
= a - 3b
|
and similarly
(b)
| (7 x + 5 y ) -
(2 x - 3 y ) |
= 7 x + 5 y - 2 x - ( - 3 y ) = 7 x +
5 y - 2 x + 3 y
= 7 x - 2 x + 5 y + 3 y
= 5 x + 8 y .
|
When there is more than one bracket it is usually necessary to
begin with the inside bracket and work outwards.
Example 2
Simplify the following expressions by removing the brackets.
(a) 3 a - c + (5 a - 2 b - [3 a - c + 2 b]),
(b) -{3 y - (2 x - 3 y) + (3 x - 2 y)} + 2 x.
Solution
(a) We have
| 3 a - c + (5 a
- 2 b - [3 a - c + 2 b]) |
= 3 a - c + (5 a - 2 b - 3 a + c - 2 b) =
3 a - c + (2 a - 4 b + c)
= 3 a - c + 2 a - 4 b + c
= 3 a + 2 a - 4 b - c + c
= 5 a - 4 b .
|
(b) Similarly we have
| -3 y - (2 x -
3 y) + (3 x - 2 y) + 2 x |
= -3 y - 2 x + 3 y + 3 x - 2 y + 2 x =
-3 y + 3 y - 2 y + 3 x - 2 x + 2 x
= -4 y + x + 2 x
= -4 y - x + 2 x
= x - 4 y .
|
Exercise
Remove the brackets from each of the
following expressions and simplify as far as
possible.
(a) x - ( y - z ) + x + ( y - z ) - ( z + x )
,
(b) 2 x - (5 y + [3 z - x] ) - (5 x - [ y + z
] ),
(c) (3 /a) + b + (7 /a) - 2 b,
(d) a - ( b + [ c - {a - b}] ) .
Solution
(a)
x - ( y - z ) + x + ( y - z ) - ( z + x )
= x - y + z + x + y - z - z - x
= x + x - x - y + y + z - z - z
= x - z .
(b)
2 x - (5 y + [3 z - x ]) - (5 x - [ y + z ])
= 2 x - (5 y + 3 z - x ) - (5 x - y - z )
= 2 x - 5 y - 3 z + x - 5 x + y + z
= 2 x + x - 5 x - 5 y + y - 3 z + z
= - 2 x - 4 y - 2 z .
(c)
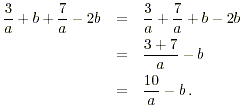
(d)
a - ( b + [ c - { a - b } ])
= a - ( b + [ c - a + b ])
= a - ( b + c - a + b )
= a - (2 b + c - a )
= a - 2 b - c + a
= 2 a - 2 b - c .
|