Rationalizing Denominators
The next example shows how to rationalize (remove all radicals
from) the denominator in an expression containing radicals.
EXAMPLE 3
Rationalizing the Denominator
Simplify each of the following expressions by rationalizing
the denominator.
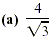
Solution
To rationalize the denominator, multiply by 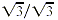 (or 1) so that the denominator of the product is a
rational number. (or 1) so that the denominator of the product is a
rational number.
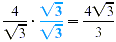
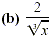
Solution
Here, we need a perfect cube under the radical sign to
rationalize the denominator. Multiplying by 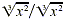 gives gives
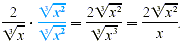
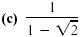
Solution
The best approach here is to multiply both numerator and
denominator by the number 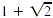 . The expressions . The expressions 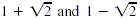 are conjugates. (If a and b are real numbers, the
conjugate of a + b is a - b.) Thus, are conjugates. (If a and b are real numbers, the
conjugate of a + b is a - b.) Thus,
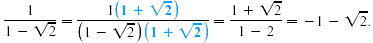
Sometimes it is advantageous to rationalize the numerator of a
rational expression. The following example arises in calculus
when evaluating a limit.
EXAMPLE 4
Rationalizing the Numerator
Rationalize the numerator.
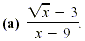
Solution
Multiply numerator and denominator by the conjugate of the
numerator, 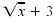 . .
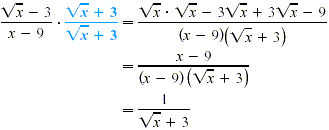
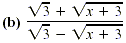
Solution
Multiply the numerator and denominator by the conjugate of the
numerator, 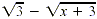
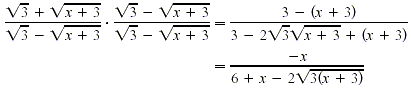
When simplifying a square root, keep in mind that 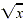 is positive by definition. Also, is positive by definition. Also, 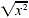 is not x, but the absolute value of , defined as is not x, but the absolute value of , defined as
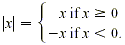
For example, 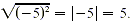
EXAMPLE 5
Simplifying by Factoring
Simplify 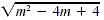 . .
Solution
Factor the polynomial as 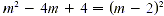 . Then by property 2 of radicals, and the definition
of absolute value, . Then by property 2 of radicals, and the definition
of absolute value,
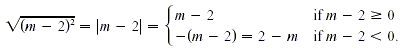
CAUTION
Avoid the common error of writing 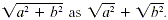 We must add We must add 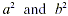 before taking the square root. For example, before taking the square root. For example, 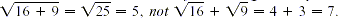 This idea applies as well to higher roots. For
example, in general, This idea applies as well to higher roots. For
example, in general,
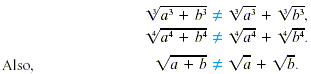
|