Variables and Expressions
After completing this lesson, you will be able to:
- Write mathematical expressions using verbal expressions
- Define variable and algebraic expression
In algebra, letters are often used to represent numbers. These
are called variables. An algebraic
expression is a mathematical statement which at least
one number and at least one variable along with at least one
arithmetic operation.
Example 1
Write an algebraic expression for the difference of x and 7.
The word difference means subtract, so the algebraic
expression would be x - 7
This is an algebraic expression because it contains at least
one number (7), at least one variable (x), and at least one
arithmetic operation (subtraction).
Example 2
Write an algebraic expression for the number y added to 4
times the number x.
This would be written as y + 4x
The 4x means 4 times the number x
Example 3
Write an algebraic expression for the sum of twelve and the
product of five and x.
The word sum means to add.
The word product means to multiply.
Therefore, our algebraic expression would be 12 + 5x
Example 4
Write a verbal expression for z + 10.
This time, we are taking an algebraic expression and
translating it to a verbal expression.
The term for + is sum. Therefore, we would write the sum of z
and ten
Example 5
Write a verbal expression for 10xy. Since the only operation
here is multiplication, we could write ten times x times y or we
Could write times the product of x and y. Either expression is
correct.
In the expression 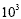 , 10 is called the base and 3 is called the exponent
. The meaning of this expression is 10 · 10 · 10 . If you were
asked to find the answer you would multiply 10 · 10 · 10 and
get 1000. This is called evaluating the expression. The algebraic
expression 4 · x · x · x · y · y could be written using
exponents. The new expression would be , 10 is called the base and 3 is called the exponent
. The meaning of this expression is 10 · 10 · 10 . If you were
asked to find the answer you would multiply 10 · 10 · 10 and
get 1000. This is called evaluating the expression. The algebraic
expression 4 · x · x · x · y · y could be written using
exponents. The new expression would be 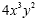 . The algebraic expression 4 · 4 · x · y · y ·
y could be written using exponents. The new expression would be . The algebraic expression 4 · 4 · x · y · y ·
y could be written using exponents. The new expression would be 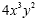 or it could also be written or it could also be written 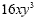 because because 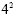 is the same as 16. is the same as 16.
Example 6
Evaluate the expression 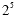 Evaluate simply means that we want to find an
answer. Remember that Evaluate simply means that we want to find an
answer. Remember that 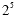 means 2 · 2 · 2 · 2 · 2 . (It does not mean 2
times 5). Since 2 · 2 · 2 · 2 · 2 is 32, that is the answer. means 2 · 2 · 2 · 2 · 2 . (It does not mean 2
times 5). Since 2 · 2 · 2 · 2 · 2 is 32, that is the answer.
|