Product and Quotient of Functions
We may also evaluate the product or quotient of two functions by another method. That is, we first evaluate each function, and then we multiply or divide.
Example 1
Given f(x) = x2 - 13 and g(x) = x + 9, find (f
· g)(x) when x = -4.
That is, find (f · g)(-4).
Solution
| Step 1 |
Use x = -4 to find f(-4) and g(-4).
Substitute -4 for x in f(x).
Simplify.
So, f(-4) = 3.
Substitute -4 for x in g(x).
Simplify.
So, g(-4) = 5. |
f(-4)
g(-4) |
= (-4)2 - 13
= 3
= (-4) + 9
= 5 |
| Step 2 |
Find f(-4) · g(-4).
Multiply. |
f(-4)
· g(-4) |
= 3 · 58 |
So, (f · g)(-4) = 15.
Example 2
Given f(x) = 3x2 - 8 and g(x) = x + 19, find
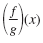 when x
= 6. That is, find
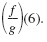
Solution
| Step 1 |
Use x = 6 to find f(6) and g(6). Substitute 6 for x in f(x).
Simplify.
So, f(6) = 100.
Substitute 6 for x in g(x).
Add.
So, g(6) = 25. |
f(6)
g(6) |
= 3(6)2 - 8
= 100
= (6) + 19
= 25 |
| Step 2 |
Find
 |
 |
 |
| |
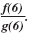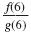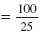Divide. |
|
= 4 |
So,
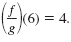
Note:
This method is preferred by many students for
evaluating the sum, difference, product, or
quotient of two functions. This is because
numbers are substituted immediately and
so the calculations are often easier.
|
