Dividing With Fractions
First, we need some terminology. When we wish to divide one
quantity by another, the quantity that we are dividing by
is called the divisor, and the quantity being
divided is call the dividend. The result of the
operation is sometimes called the quotient (although
the word “quotient” is used in other ways in
mathematics as well).
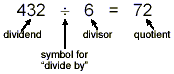
When we invert a fraction, interchanging the
numerator and denominator, we get the reciprocal
of the original fraction:
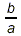 is the reciprocal of is the reciprocal of 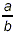
Thus, for example
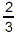 is the reciprocal of is the reciprocal of 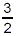
and
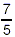 is the reciprocal of is the reciprocal of 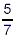
From the rule for multiplying two fractions together, you see
that when we multiply a fraction by its reciprocal, we get the
result 1:
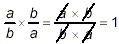
(Some people use the term “inverse” to refer to the
reciprocal of a fraction, but this should not be done in general,
because the word “inverse” actually usually means
something else in mathematics.)
The procedure for dividing by a fraction is now easy to state
in words: to divide by a fraction, you just invert this divisor
and multiply. So dividing by a fraction is done as multiplying by
its reciprocal. The multiplication is done exactly as described
in the previous note in this series. So, for example,
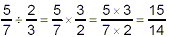
In symbols, we can write
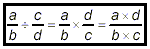
Examples:
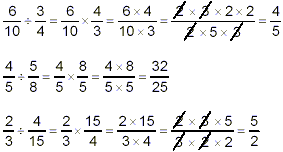
In the first and third examples here, we factored the factors
after the multiplication step to check for possible
simplification of the result. In the second example, we could see
that there was no possibility of simplification, because 5 is
obviously not a factor of either 4 or 8.
Common Error
Quite often people have a vague recollection that division by
a fraction involves flipping the fraction and maybe something
like multiplying numerators and denominators together, or
something like that. Then they end up doing something along the
following lines:
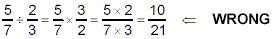
mixing numerators and denominators in the multiplication step.
This gives entirely the wrong answer. You must do the
multiplication step just like you would multiply any other pair
of fractons together.
Another Way of Writing Division by a Fraction
Since the form of a fraction represents the result of division
of the numerator by the denominator, we can also represent
division by a fraction as a fractional expression in which the
numerator is the dividend value and the denominator is the
divisor value. For example
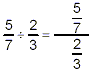
Later in these notes, we will indicate that expressions such
as the one on the right above are called complex
fractions because they are a fraction whose parts
contain other fractions. This form does give a way to demonstrate
that the rule for dividing by a fraction is consistent with
properties we’ve previously discovered about fractions. To
try to simplify the complex fraction above, start by multiplying
the numerator and denominator by the reciprocal of the
denominator:
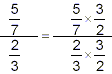
This gives an equivalent fraction, since we are multiplying
the numerator and denominator by the same value. The thing is,
the new denominator, which is the product of the original
denominator and its reciprocal, simplifies to 1:
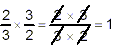
and so
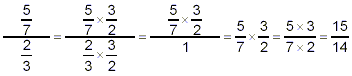
when we drop the denominator of 1 (which can always be done
because of the property that 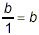 for any number b). We get exactly the
same result as we would have obtained using the original rule for
dividing by a fraction. This example illustrates why the invert
and multiply rule works for dividing by a fraction. for any number b). We get exactly the
same result as we would have obtained using the original rule for
dividing by a fraction. This example illustrates why the invert
and multiply rule works for dividing by a fraction.
Division With Mixed Numbers
As has been true of all other arithmetic operations, division
with mixed numbers requires you to first convert the mixed
numbers to pure fractions and then apply the methods appropriate
for fractions.
Example:
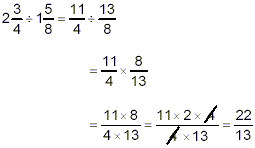
|