Locating the Solutions of the Quadratic Equation
Once you have manipulated the quadratic inequality so that it resembles one of the four
forms, the next step is to use the quadratic formula to locate the solutions of the equation:
a · x2 + b
· x + c = 0.
The quadratic formula:
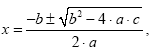
is appropriate for solving this equation.
It is useful to think of
y = ax2 + bx + c
as a parabolic graph (a smile or a frowm) that passes through the two points on the x-axis
determined by the solutions to the quadratic equation.
If you discover that the quadratic equation has no solutions, then the quadratic
inequality that you are trying to solve either has no solutions or every real number x
solves the inequality. The parabola is either a smile (a>0) which lies above the x-axis,
or a frown (a<0) that lies below.
For example if (a>0) so that the parabola is a smile, then every real number x solves
ax2 + bx + c > 0,
and there are no solutions to
ax2 + bx + c < 0.
If you discover that the quadratic equation has exactly one solution, then the
quadratic
inequality that you trying to solve could have no solutions, exactly one solution, or
every real number x could be a solution. In this case the parabola has its vertex at the
point on the x-axis given by the quadratic formula. The graph of the parabola is either a
smile (a > 0) with its vertex on the x-axis, or a frown (a < 0) with its vertex on the x-axis.
The inequalities can now be analyzed in a similar way to the above. If the quadratic
equation has only one solution, say x = p, then the vertex of the parabola is at (p, 0). If
for example a < 0 (a frown), then every value x solves
ax2 + bx + c
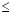 0. 0.
Every value x except x = p solves
ax2 + bx + c < 0 (x = p is not a solution)
There are no solutions to
ax2 + bx + c > 0,
and only x = p solves the inequality
ax2 + bx + c
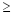 0. 0.
The case a>0 can be handled in similar way by simply viewing the parabola as a smile
with vertex on the x-axis.
|